题目内容
已知函数f（x）=x2，g（x）=x-1，若存在x∈R，使f（x）＜b•g（x），则b的范围是（ ）
| A、（-∞，0）∪（4，+∞） |
| B、（4，+∞） |
| C、（-∞，0） |
| D、（0，4） |
考点：二次函数的性质
专题：函数的性质及应用
分析：若存在x∈R，使f（x）＜b•g（x），即f（x）-b•g（x）=x2-b（x-1）=x2-bx+b＜0有解，即△=b2-4b＞0，解得答案．
解答：
解：存在所代表的意思是只要有一个实数满足就可以，
令f（x）-b•g（x）=x2-b（x-1）=x2-bx+b＜0
则△=b2-4b＞0，
解得：b∈（-∞，0）∪（4，+∞），
故选：A
令f（x）-b•g（x）=x2-b（x-1）=x2-bx+b＜0
则△=b2-4b＞0，
解得：b∈（-∞，0）∪（4，+∞），
故选：A
点评：本题考查的知识点是二次函数的图象和性质，二次不等式的解法，难度不大，属于基础题．
练习册系列答案
相关题目
已知函数y=ex图象记为曲线C1，O为坐标系原点
Ⅰ）过O作曲线C1的切线l，求切线l的方程；
Ⅱ）函数y=lnx图象记为曲线C2，点P在曲线C1上，点Q在曲线C2上，设∠POQ=θ，求cosθ的最大值．
Ⅰ）过O作曲线C1的切线l，求切线l的方程；
Ⅱ）函数y=lnx图象记为曲线C2，点P在曲线C1上，点Q在曲线C2上，设∠POQ=θ，求cosθ的最大值．
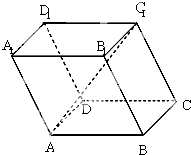已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1的长为2，∠A1AB=∠A1AD=120°．