题目内容
已知圆C:(x-a)2+(y-b)2=r2(b>0),圆心在抛物线y2=4x上,经过点A(3,0),且与抛物线的准线相切,则圆C的方程为 .
考点:抛物线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:由已知结合抛物线的性质,可得C到抛物线y2=4x准线的距离等于C到点A(3,0)的距离,即C到抛物线y2=4x焦点F(1,0)的距离等于C到点A(3,0)的距离,故C点在FA的垂直平方线x=2上,进而可得圆心坐标和半径,求得答案.
解答:
解:∵圆C:(x-a)2+(y-b)2=r2(b>0)与抛物线y2=4x的准线相切,经过点A(3,0),
∴C到抛物线y2=4x准线的距离等于C到点A(3,0)的距离,
即C到抛物线y2=4x焦点F(1,0)的距离等于C到点A(3,0)的距离,
∴C点在FA的垂直平方线x=2上,
故圆C的半径为3,
又∵C在抛物线y2=4x上,b>0
∴b=2
,
故圆C的方程为:(x-2)2+(y-2
)2=9,
故答案为:(x-2)2+(y-2
)2=9
∴C到抛物线y2=4x准线的距离等于C到点A(3,0)的距离,
即C到抛物线y2=4x焦点F(1,0)的距离等于C到点A(3,0)的距离,
∴C点在FA的垂直平方线x=2上,
故圆C的半径为3,
又∵C在抛物线y2=4x上,b>0
∴b=2
| 2 |
故圆C的方程为:(x-2)2+(y-2
| 2 |
故答案为:(x-2)2+(y-2
| 2 |
点评:本题考查的知识点是抛物线的性质,圆的标准方程,是抛物线与圆的综合应用,难度中档.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
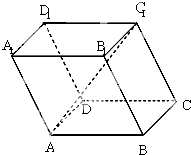 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.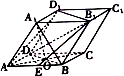 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=