题目内容
已知直线l1:mx-y=0,l2:x+my-m-2=0,m∈R.
(1)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(2)若l1与(1)中的定圆的另一个交点为P1,l2与(1)中的定圆的另一个交点为P2,求△PP1P2面积取得最大值,并求出此时直线l1的方程.
(1)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(2)若l1与(1)中的定圆的另一个交点为P1,l2与(1)中的定圆的另一个交点为P2,求△PP1P2面积取得最大值,并求出此时直线l1的方程.
考点:直线和圆的方程的应用,直线的一般式方程
专题:直线与圆
分析:(1)联立两条直线方程,消去m,即得到l1和l2的交点M的方程,判断M总在一个定圆上即可;
(2)通过l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,利用(2)说明P1P2是圆C的直径,当且仅当圆心C(1,
)到l1的距离等于C到l2的距离时,△MP1P2面积取得最大值,利用点到直线的距离公式列出m的关系式,求出m即可得到直线l1的方程.
(2)通过l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,利用(2)说明P1P2是圆C的直径,当且仅当圆心C(1,
| 1 |
| 2 |
解答:
证明:(1)由题意可得
,
消去m可得x2+y2-2x-y=0,
方程表示一个以(1,
)为圆心,以
为半径的圆,
即M总在一个定圆上.
解:(2)由圆C的方程以及直线l1的方程可知,
直线l1恒过(0,0)点,
方程l2:x+my-m-2=0可化为(x-2)+m(y-1)=0,
∵对于任意实数m直线l2:x+my-m-2=0 恒过定点
∴x-2=y-1=0,
∴直线l2恒过(2,1)点,
故直线l1,l2的与圆C的另一个交点P1(0,0),P2(2,1),
∵P1P2是圆C的直径,
当且仅当圆心C(1,
)到l1的距离等于C到l2的距离时,△MP1P2面积取得最大值,
所以
=
,
解得:m=3或m=-
,
所以直线l1:3x-y=0或x+3y=0.
|
消去m可得x2+y2-2x-y=0,
方程表示一个以(1,
| 1 |
| 2 |
| ||
| 2 |
即M总在一个定圆上.
解:(2)由圆C的方程以及直线l1的方程可知,
直线l1恒过(0,0)点,
方程l2:x+my-m-2=0可化为(x-2)+m(y-1)=0,
∵对于任意实数m直线l2:x+my-m-2=0 恒过定点
∴x-2=y-1=0,
∴直线l2恒过(2,1)点,
故直线l1,l2的与圆C的另一个交点P1(0,0),P2(2,1),
∵P1P2是圆C的直径,
当且仅当圆心C(1,
| 1 |
| 2 |
所以
|m-
| ||
|
|
| ||
|
解得:m=3或m=-
| 1 |
| 3 |
所以直线l1:3x-y=0或x+3y=0.
点评:本题通过恒过定点问题来考查学生方程转化的能力及直线系的理解,曲线轨迹方程的求法,三角形的面积的最值的判断,考查计算能力,转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
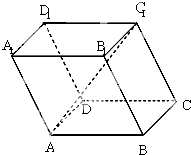 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.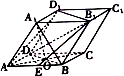 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=