题目内容
长为6的线段AB两端点在抛物线x2=4y上移动,在线段AB中点纵坐标的最小值为 .
考点:抛物线的简单性质
专题:空间位置关系与距离
分析:如图所示,设线段AB的中点为M,分别过点A,B,C,作AD⊥x轴,BE⊥x轴,MN⊥x轴,垂足分别为D,E,N.利用梯形的中位线和抛物线的定义可得|MN|=
(|AD|+|BE|)=
(|AF|-1+|BF|-1)≥
(|AB|-2)即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:如图所示,设线段AB的中点为M,

分别过点A,B,C,作AD⊥x轴,BE⊥x轴,MN⊥x轴,垂足分别为D,E,N.
则|MN|=
(|AD|+|BE|)=
(|AF|-1+|BF|-1)≥
(|AB|-2)=
(6-2)=2.
当且仅当线段AB过焦点时取等号.
故AB的中点到y轴的距离的最小值为2.
故答案为:2

分别过点A,B,C,作AD⊥x轴,BE⊥x轴,MN⊥x轴,垂足分别为D,E,N.
则|MN|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当线段AB过焦点时取等号.
故AB的中点到y轴的距离的最小值为2.
故答案为:2
点评:本题考查了抛物线的定义和梯形的中位线定理,考查了分析问题和解决问题的能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
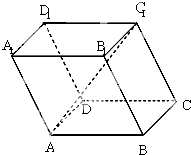 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.