题目内容
记数列{an}的前n项和为Sn(n∈N*),若存在实常数A,B,C,对于任意正整数n,都有an+Sn=An2+Bn+C成立.
(1)已知A=B=0,a1≠0,求证:数列{an}(n∈N*)是等比数列;
(2)已知数列{an}(n∈N*)是等差数列,求证:3A+C=B;
(3)已知a1=1,B>0且B≠1,B+C=2.设λ为实数,若?n∈N*,
<λ,求λ的取值范围.
(1)已知A=B=0,a1≠0,求证:数列{an}(n∈N*)是等比数列;
(2)已知数列{an}(n∈N*)是等差数列,求证:3A+C=B;
(3)已知a1=1,B>0且B≠1,B+C=2.设λ为实数,若?n∈N*,
| an |
| an+1 |
考点:等比关系的确定,等差数列的性质,数列递推式
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)由an+Sn=C(n∈N*),an+1+Sn+1=C.得an+1=2an,故数列{an}(n∈N*)是等比数列;
(2)令公差为d,根据等差数列的通项公式和前n项和公式,得到
n2+(a1+
)n+a1-d=An2+Bn+C.问题得以证明
(3)根据题意到数列的递推公式,再分类讨论,求出λ的范围
(2)令公差为d,根据等差数列的通项公式和前n项和公式,得到
| d |
| 2 |
| d |
| 2 |
(3)根据题意到数列的递推公式,再分类讨论,求出λ的范围
解答:
解:(1)由A=B=0,得an+Sn=C(n∈N*),①
从而an+1+Sn+1=C. ②…2分
②-①式得an+1=2an,
又a1≠0,所以数列{an}为等比数列.
(2)由数列{an}是等差数列,可令公差为d,则an=a1+(n-1)d,Sn=na1+
d.
于是由an+Sn=An2+Bn+C得
n2+(a1+
)n+a1-d=An2+Bn+C.
由正整数n的任意性得
从而得3A+C=
+a1-d=a1+
=B.
(3)由a1=1,B+C=2,及an+Sn=An2+Bn+C,得2a1=A+B+C,即2=A+B+C,
则有A=0.
于是an+Sn=Bn+(2-B),从而an+1+Sn+1=B(n+1)+(2-B),
相减得2an+1-an=B,an+1-B=
(an-B),
又a1=1,B≠1,则a1-B≠0,
所以an-B=(a1-B)
,即an=(1-B)
+B.
于是
=
=1+
.
由B>0且B≠1,下面需分两种情形来讨论.
(i)当0<B<1时,1-B>0,则式子
的值随n的增大而减小,
所以,对?n∈N*,
的最大值在n=1时取得,即(
)max═1+
=
.
于是,对于?n∈N*,
≤
,
又
<λ,
∴λ>
.
(ii)当B>1时,由(1-B)+2nB≥(1-B)+2B=1+B>0,2nB≥2B>2B-1,
得-1<
<0.
所以,对于?n∈N*,0<
=1+
<1. ①
假设λ<1,则有λ>0,且
=1+
<λ,
得2n<
,即n<log2
,
这表明,当n取大于等于log2
的正整数时,
<λ不成立,
与题设不符,矛盾.所以λ≥1.又由①式知λ≥1符合题意.
故B>1时,λ≥1.
综上所述,当0<B<1时,λ>
;当B>1时,λ≥1.
从而an+1+Sn+1=C. ②…2分
②-①式得an+1=2an,
又a1≠0,所以数列{an}为等比数列.
(2)由数列{an}是等差数列,可令公差为d,则an=a1+(n-1)d,Sn=na1+
| n(n-1) |
| 2 |
于是由an+Sn=An2+Bn+C得
| d |
| 2 |
| d |
| 2 |
由正整数n的任意性得
|
从而得3A+C=
| 3d |
| 2 |
| d |
| 2 |
(3)由a1=1,B+C=2,及an+Sn=An2+Bn+C,得2a1=A+B+C,即2=A+B+C,
则有A=0.
于是an+Sn=Bn+(2-B),从而an+1+Sn+1=B(n+1)+(2-B),
相减得2an+1-an=B,an+1-B=
| 1 |
| 2 |
又a1=1,B≠1,则a1-B≠0,
所以an-B=(a1-B)
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
于是
| an |
| an+1 |
(1-B)
| ||
(1-B)
|
| 1-B |
| (1-B)+2nB |
由B>0且B≠1,下面需分两种情形来讨论.
(i)当0<B<1时,1-B>0,则式子
| 1-B |
| (1-B)+2nB |
所以,对?n∈N*,
| an |
| an+1 |
| an |
| an+1 |
| 1-B |
| (1-B)+2nB |
| 2 |
| 1+B |
于是,对于?n∈N*,
| an |
| an+1 |
| 2 |
| 1+B |
又
| an |
| an+1 |
∴λ>
| 2 |
| 1+B |
(ii)当B>1时,由(1-B)+2nB≥(1-B)+2B=1+B>0,2nB≥2B>2B-1,
得-1<
| 1-B |
| (1-B)+2nB |
所以,对于?n∈N*,0<
| an |
| an+1 |
| 1-B |
| (1-B)+2nB |
假设λ<1,则有λ>0,且
| an |
| an+1 |
| 1-B |
| (1-B)+2nB |
得2n<
| (B-1)(2-λ) |
| (1-λ)B |
| (B-1)(2-λ) |
| (1-λ)B |
这表明,当n取大于等于log2
| (B-1)(2-λ) |
| (1-λ)B |
| an |
| an+1 |
与题设不符,矛盾.所以λ≥1.又由①式知λ≥1符合题意.
故B>1时,λ≥1.
综上所述,当0<B<1时,λ>
| 2 |
| 1+B |
点评:本题属于数列综合运用题,考查了由所给的递推关系证明数列的性质,对所给的递推关系进行研究求数列的递推公式以及利用数列的求和公式求其和,再由和的存在范围确定使得不等式成立的参数的取值范围,难度较大,综合性很强,对答题者探究的意识与探究规律的能力要求较高,是一道能力型题.

练习册系列答案
相关题目
一组数据用茎叶图表示如图,则这组数据的中位数是( )


| A、23 | B、25 | C、36 | D、34 |
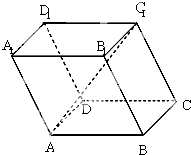 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.