题目内容
11. 据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.
据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2${\;}^{11-\frac{t}{2}}$,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
分析 (1)由图象知函数图象过(5,1),(7,2),得到$\left\{\begin{array}{l}{(1-\frac{k}{8})(5-b)^{2}=0}\\{(1-\frac{k}{8})(7-b)^{2}=1}\end{array}\right.$,解得即可.
(2)能根据题意构造函数,并能在定义域内求函数的最小值.
解答 解:(1)由图象知函数图象过(5,1),(7,2),
∴$\left\{\begin{array}{l}{(1-\frac{k}{8})(5-b)^{2}=0}\\{(1-\frac{k}{8})(7-b)^{2}=1}\end{array}\right.$,解得k=6,b=5;
(2)当P=Q时,${2}^{(1-6t)(x-5)^{2}}$=2${\;}^{11-\frac{x}{2}}$,即(1-6t)(x-5)2=11-$\frac{x}{2}$,
即2-12t=$\frac{22-x}{(x-5)^{2}}$,
令m=$\frac{1}{x-5}$(0<m≤$\frac{1}{5}$),则2(1-6t)=17m2-m=17(m-$\frac{1}{34}$)2-$\frac{1}{68}$,
∴m=$\frac{1}{5}$时,2(1-6t)max=$\frac{12}{25}$
∴1-6t≤$\frac{6}{25}$,
即t≥$\frac{19}{150}$,
∴税率t=$\frac{19}{150}$时,平衡价格为10元.
点评 此题是个指数函数的综合题,但在求解的过程中也用到了构造函数的思想及二次函数在定义域内求最值的知识,属于中档题

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
1.将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,所得函数的解析式为( )
| A. | $y=sin({2x+\frac{5π}{6}})$ | B. | y=-cos2x | C. | y=cos2x | D. | $y=sin({2x-\frac{π}{6}})$ |
19.若函数f(x)=sin(x+φ)是偶函数,则φ可取一个值为( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
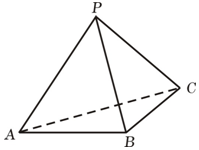 如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.
如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.