题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,且该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
+2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)记椭圆C的上顶点为B,直线l交椭圆C于P,Q两点,问:是否存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心(△PQB三条边上的高线的交点)?若存在,求出直线l的方程,若不存在,请说明理由.
(Ⅲ)若⊙M是以AF2为直径的圆,求证:⊙M与以坐标原点为圆心,a为半径的圆相内切.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)记椭圆C的上顶点为B,直线l交椭圆C于P,Q两点,问:是否存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心(△PQB三条边上的高线的交点)?若存在,求出直线l的方程,若不存在,请说明理由.
(Ⅲ)若⊙M是以AF2为直径的圆,求证:⊙M与以坐标原点为圆心,a为半径的圆相内切.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(I)由椭圆C:
+
=1(a>b>0)的离心率为
,可得
=
.该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
+2,可得|AF1|+|AF2|+|F1F2|=2a+2c=2
+2.及b=
联立解得即可.
(II)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心.设P(x1,y1),Q(x2,y2).则BF2⊥PQ.
由kBF2=-1,可得kPQ=1.设直线l的方程为:y=x+m,与椭圆的方程联立可得根与系数的关系,再利用
⊥
,可得
•
=x1(x2-1)+y2(y1-1)=0,解得m即可.
(III)证明设A(x0,y0),F2(1,0),则M(
,
),设两圆的半径分别为r1,r2.|OM|=
=
+
x0.又⊙M的半径r1=|MF2|=
-
x0.r2=a=
.只要证明|OM|=r2-r1.即可.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
| 2 |
| a2-c2 |
(II)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心.设P(x1,y1),Q(x2,y2).则BF2⊥PQ.
由kBF2=-1,可得kPQ=1.设直线l的方程为:y=x+m,与椭圆的方程联立可得根与系数的关系,再利用
| BP |
| QF2 |
| BP |
| QF2 |
(III)证明设A(x0,y0),F2(1,0),则M(
| x0+1 |
| 2 |
| y0 |
| 2 |
(
|
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| 2 |
解答:
解:(I)∵椭圆C:
+
=1(a>b>0)的离心率为
,
∴
=
,
该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
+2,
∴|AF1|+|AF2|+|F1F2|=2a+2c=2
+2.
解得a=
,c=1,∴b=
=1.
∴椭圆C的方程为
+y2=1.
(II)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心.
设P(x1,y1),Q(x2,y2).则BF2⊥PQ.
∵B(0,1),F2(1,0),∴kBF2=-1,∴kPQ=1.
设直线l的方程为:y=x+m,联立
,
化为3x2+4mx+2m2-2=0,则x1+x2=-
,x1x2=
.(*).
∵
⊥
,
∴x1(x2-1)+y2(y1-1)=0,
∴x1(x2-1)+(x2+m)(x1+m-1)=0,化为2x1x2+(x1+x2)(m-1)+m2-m=0,
∴
-
+m2-m=0,化为3m2+m-4=0,解得m=-
,m=1.
经检验m=-
符合条件,直线l的方程为y=x-
.
(III)证明:设A(x0,y0),F2(1,0),则M(
,
),
设两圆的半径分别为r1,r2.
|OM|=
=
=
+
x0.
又⊙M的半径r1=|MF2|=
-
x0.r2=a=
.
∴r2-r1=
-(
-
x0)=
+
x0.
∴|OM|=r2-r1.
∴⊙M与以坐标原点为圆心,a为半径的圆相内切.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
| 2 |
∴|AF1|+|AF2|+|F1F2|=2a+2c=2
| 2 |
解得a=
| 2 |
| a2-c2 |
∴椭圆C的方程为
| x2 |
| 2 |
(II)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心.
设P(x1,y1),Q(x2,y2).则BF2⊥PQ.
∵B(0,1),F2(1,0),∴kBF2=-1,∴kPQ=1.
设直线l的方程为:y=x+m,联立
|
化为3x2+4mx+2m2-2=0,则x1+x2=-
| 4m |
| 3 |
| 2m2-2 |
| 3 |
∵
| BP |
| QF2 |
∴x1(x2-1)+y2(y1-1)=0,
∴x1(x2-1)+(x2+m)(x1+m-1)=0,化为2x1x2+(x1+x2)(m-1)+m2-m=0,
∴
| 4m2-4 |
| 3 |
| 4m(m-1) |
| 3 |
| 4 |
| 3 |
经检验m=-
| 4 |
| 3 |
| 4 |
| 3 |
(III)证明:设A(x0,y0),F2(1,0),则M(
| x0+1 |
| 2 |
| y0 |
| 2 |
设两圆的半径分别为r1,r2.
|OM|=
(
|
|
| ||
| 2 |
| ||
| 4 |
又⊙M的半径r1=|MF2|=
| ||
| 2 |
| ||
| 4 |
| 2 |
∴r2-r1=
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
∴|OM|=r2-r1.
∴⊙M与以坐标原点为圆心,a为半径的圆相内切.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、两点之间的距离公式、两圆相内切的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知某个几何体的三视图如右图,根据图中标出的尺寸可得这个几何体的体积是( )
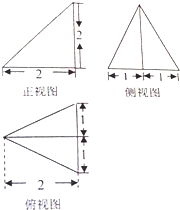

A、
| ||
B、
| ||
C、
| ||
D、
|
若方程|2x-2|-a=0有两个解,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,2) | D、∅ |