题目内容
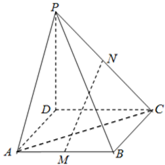 如图,P是正方形ABCD所在平面外一点,且PD⊥AD,PD⊥DC,PD=3,AD=2,若M、N分别是AB、PC的中点.
如图,P是正方形ABCD所在平面外一点,且PD⊥AD,PD⊥DC,PD=3,AD=2,若M、N分别是AB、PC的中点.(1)求证:MN⊥DC;
(2)求点M到平面PAC的距离.
考点:点、线、面间的距离计算
专题:计算题,证明题,空间位置关系与距离
分析:(1)建立空间直角坐标系,利用MN,DC对应的向量的数量积为0,证明两条直线垂直;
(2)求出平面PAC的法向量,求出
,然后利用向量在平面单位法向量方向投影长度,求解求点M到平面PAC的距离.
(2)求出平面PAC的法向量,求出
| MA |
解答:
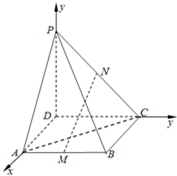 (本小题满分13分)
(本小题满分13分)
解:如图建系,则D(0,0,0),
A(2,0,0),B(2,2,0),C(0,2,0),P(0,0,3),则M(2,1,0),N(0,1,
).
(1)∴
=(-2,0,
),
=(0,2,0)∴
•
=(-2,0,
)•(0,2,0)=0,∴MN⊥DC.
(2)设
=(x,y,z)为平面PAC的一个法向量,
=(2,0,-3),
=(0,2,-3),
由
,得
取x=3,则y=3,z=2,
=(3,3,2),
=(-1,0,0)
∴d=
=
=
,
∴点M到平面PAC的距离为
.
 (本小题满分13分)
(本小题满分13分)解:如图建系,则D(0,0,0),
A(2,0,0),B(2,2,0),C(0,2,0),P(0,0,3),则M(2,1,0),N(0,1,
| 3 |
| 2 |
(1)∴
| MN |
| 3 |
| 2 |
| DC |
| MN |
| DC |
| 3 |
| 2 |
(2)设
| n |
| PA |
| PC |
由
|
|
取x=3,则y=3,z=2,
| n |
| MA |
∴d=
|
| ||||
|
|
| 3 | ||
|
3
| ||
| 22 |
∴点M到平面PAC的距离为
3
| ||
| 22 |
点评:本题考查向量方法求解点到平面的距离以及向量的数量积判断直线与直线的垂直,考查空间想象能力以及计算能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
圆C:x2+y2-2x-4y+4=0的圆心到直线l:3x+4y+4=0的距离为( )
A、3
| ||
| B、2 | ||
| C、3 | ||
D、
|
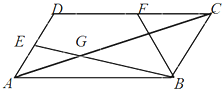 如图所示,在平行四边形ABCD中,∠BAD=
如图所示,在平行四边形ABCD中,∠BAD=