题目内容
已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12
(1)证明:不论k取任何实数,直线l与圆C总有两个交点;
(2)求直线l:y=kx+1恒过的定点;
(3)求直线l被圆C截得的最短弦长.
(1)证明:不论k取任何实数,直线l与圆C总有两个交点;
(2)求直线l:y=kx+1恒过的定点;
(3)求直线l被圆C截得的最短弦长.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)直线y=kx+1的定点(0,1)在圆内,可得不论k取任何实数,直线l与圆C总有两个交点;
(2)令x=0,可得y=1,即可得出结论;
(3)过圆内定点P(0,1)的弦,只有和PC(C是圆心)垂直时才最短.
(2)令x=0,可得y=1,即可得出结论;
(3)过圆内定点P(0,1)的弦,只有和PC(C是圆心)垂直时才最短.
解答:
(1)证明:令x=0,可得y=1,∴直线y=kx+1的定点(0,1).
∵(0-1)2+(1+1)2=5<12,
∴(0,1)在圆内,
∴不论k取任何实数,直线l与圆C总有两个交点;
(2)解:由(1)知,直线y=kx+1的定点(0,1);
(3)解:过圆内定点P(0,1)的弦,只有和PC(C是圆心)垂直时才最短,定点P(0,1)是弦|AB|的中点,由勾股定理得,|AB|=2
=2
.
∵(0-1)2+(1+1)2=5<12,
∴(0,1)在圆内,
∴不论k取任何实数,直线l与圆C总有两个交点;
(2)解:由(1)知,直线y=kx+1的定点(0,1);
(3)解:过圆内定点P(0,1)的弦,只有和PC(C是圆心)垂直时才最短,定点P(0,1)是弦|AB|的中点,由勾股定理得,|AB|=2
| 12-5 |
| 7 |
点评:本题考查直线与圆的位置关系,考查直线恒过定点,考查学生分析解决问题的能力,确定直线恒过定点是关键.

练习册系列答案
相关题目
曲线f(x)=x2+3x在x=-1处的切线方程为( )
| A、x-y+1=0 |
| B、x-y-1=0 |
| C、2x+y+4=0 |
| D、2x+y-4=0 |
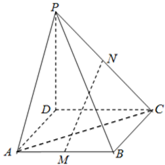 如图,P是正方形ABCD所在平面外一点,且PD⊥AD,PD⊥DC,PD=3,AD=2,若M、N分别是AB、PC的中点.
如图,P是正方形ABCD所在平面外一点,且PD⊥AD,PD⊥DC,PD=3,AD=2,若M、N分别是AB、PC的中点. 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,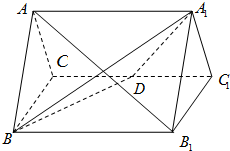 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.