题目内容
圆C：x2+y2-2x-4y+4=0的圆心到直线l：3x+4y+4=0的距离为（ ）
A、3
| ||
| B、2 | ||
| C、3 | ||
D、
|
考点：点到直线的距离公式
专题：直线与圆
分析：由圆C：x2+y2-2x-4y+4=0配方得到（x-1）2+（y-2）2=1，即可得到圆心C（1，2）．再利用圆心到直线的距离公式即可得出．
解答：
解：由圆C：x2+y2-2x-4y+4=0配方得到（x-1）2+（y-2）2=1，得到圆心C（1，2）．
∴圆心C（1，2）到直线l：3x+4y+4=0的距离d=
=3．
故选：C．
∴圆心C（1，2）到直线l：3x+4y+4=0的距离d=
| |3×1+4×2+4| | ||
|
故选：C．
点评：本题考查了圆的标准方程、配方法、点到直线的距离公式，属于基础题．
练习册系列答案
相关题目
为了判断高中三年级学生选修文科是否与性别有关，现随机抽取50名学生，得到如2×2列联表：可得到的正确结论是（ ）（Χ2=
），
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
| A、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关” |
| B、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关” |
| C、有95%以上的把握认为“爱好该项运动与性别有关” |
| D、有99%以上的把握认为“爱好该项运动与性别有关” |
已知直线l1：ax+2y-1=0与直线l2：ax-2y-3=0，“a=2”是“l1的方向向量是l2的法向量”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
双曲线x2-
=1的实轴长为（ ）
| y2 |
| 9 |
| A、4 | B、3 | C、2 | D、1 |
如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f′（5）=（ ）
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
曲线f（x）=x2+3x在x=-1处的切线方程为（ ）
| A、x-y+1=0 |
| B、x-y-1=0 |
| C、2x+y+4=0 |
| D、2x+y-4=0 |
椭圆有一个焦点固定，并通过两个已知点，且该焦点到这两个定点不等距．则该椭圆另一个焦点的轨迹类型是（ ）
| A、椭圆型 | B、双曲线型 |
| C、抛物线型 | D、非圆锥曲线型 |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜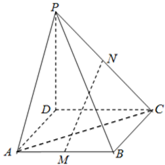
如图，P是正方形ABCD所在平面外一点，且PD⊥AD，PD⊥DC，PD=3，AD=2，若M、N分别是AB、PC的中点．