题目内容

当x→∞，下列函数均有极限，用极限与无穷小之和将他们表示出来．
（1）f（x）=
x3
x3-1
；
（2）f（x）=
1-x2
1+x2
．
考点：极限及其运算
专题：计算题
分析：（1）可将函数f（x）化为1+
1
x3-1
，再取极限即可；
（2）可将函数f（x）化为-1+
2
x2+1
，再取极限即可得到．
解答： 解：（1）f（x）=
x3
x3-1
即为f（x）=
x3-1+1
x3-1
=1+
1
x3-1
，
则
lim
x→∞
f(x)=1+
lim
x→∞
1
x3-1
=1+O（
1
x3-1
）=1；
（2）f（x）=
1-x2
1+x2
即为f（x）=-1+
2
x2+1
，
则
lim
x→∞
f(x)=-1+
lim
x→∞
2
x2+1
=-1+O（
2
x2+1
）=-1．
点评：本题考查函数的极限运算，考查将函数化简的能力，属于基础题．
练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，等比数列{bn}的前n项和为Tn，已知bn＞0（n∈N+），且a1=b1=1，a2+b3=a3，S5=5（T3+b2）．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）求和：
b2
T1•T2
+
b3
T2•T3
+…+
bn+1
Tn•Tn+1
．
一个几何体的直观图及三视图如图所示，M，N分别是AF，BC的中点．

（Ⅰ）写出这个几何体的名称；
（Ⅱ）求证：MN∥平面CDEF；
（Ⅲ）求多面体A-CDEF的体积．
如图，在△ABC中，∠A=60°，∠A的平分线交BC于D，若AB=4，且
AD
=
1
4
AC
+
λ
AB
（λ∈R），则AD的长为
 
．
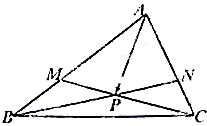在△ABC中，点M、N分别在边AB、AC上，且
AM
=2
MB
，
AN
=
3
5
AC
，线段CM与BN相交于点P，且
AB
=
a
，
AC
=
b
，则
AP
用
a
和
b
表示为（　　）
A、
AP
=
4
9
a
+
1
3
b
B、
AP
=
4
9
a
+
2
3
b
C、
AP
=
2
9
a
+
4
3
b
D、
AP
=
4
7
a
+
3
7
b
设数列{an}的前n项和为Sn，a1=1，（cosα+sinα）an+1=sinα•Sn+2cosα-sinα，（n∈N*），α∈（0，π），若对任意n∈N*，an+1＞an＞0恒成立，则α的取值范围为
 
．
过原点的直线交双曲线xy=
2
于P、Q两点，现将坐标平面沿x轴折成直二面角，则折后线段PQ的长度的最小值等于（　　）
A、4
B、2
2
C、2
D、
2
已知函数f（x）的定义域为R，且满足f（x+2）=-f（x）．若f（x）为奇函数，且当0≤x≤1时，f（x）=
1
2
x，求使f（x）=-
1
2
在[0，2 014]上的所有x的个数．
若实数a满足：a2≥2，则实数a的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网