题目内容
8.已知$\overrightarrow{a}$=(m-2,m+3),$\overrightarrow{b}$=(2m+1,m-2),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角,则实数m的取值范围是( )| A. | m>2或m<-$\frac{4}{3}$ | B. | -$\frac{4}{3}$<m<2 | C. | m≠2 | D. | m≠2且m≠-$\frac{4}{3}$ |
分析 令$\overrightarrow{a}•\overrightarrow{b}>0$解出m的范围,然后去掉向量同向时的m即可.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=(m-2)(2m+1)+(m+3)(m-2)=3m2-2m-8.
∵$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角,∴$\overrightarrow{a}•\overrightarrow{b}$>0,即3m2-2m-8>0.解得m$<-\frac{4}{3}$或m>2.
若$\overrightarrow{a},\overrightarrow{b}$同向,则$\frac{m+3}{m-2}=\frac{m-2}{2m+1}>0$,方程无解.
故m的取值范围是m$<-\frac{4}{3}$或m>2.
故选:A.
点评 本题考查了平面向量的数量积运算,向量共线的条件,属于基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
18.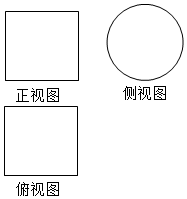 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
16.已知x0是函数f(x)=2x-log0.5x的零点.则( )
| A. | 2x0<1<x0 | B. | x0<2x0<1 | C. | 1<x0<2x0 | D. | x0<1<2x0 |