题目内容

20．柜子里有5双不同的鞋，现从柜子里取出4只鞋．求：
（1）取出的鞋中至少有一双的取法数目；
（2）取出的鞋中恰好有一双的取法数目．

分析 （1）取出的鞋中至少有一双的取法的对立事件是取出的鞋中没有是一双的取法；
（2）先从五双鞋中选出一双，有5种； 再从剩余的四双中选两只但是不能为一双，有4×6=24种，利用乘法原理即可得出结论．

解答 解：（1）取出的鞋中至少有一双的取法的对立事件是取出的鞋中没有是一双的取法，
∴取出的鞋中至少有一双的取法有${C}_{10}^{4}-{C}_{5}^{4}•{2}^{4}$=130种；
（2）先从五双鞋中选出一双，有5种；
再从剩余的四双中选两只但是不能为一双，有4×6=24种；
所以从五双不同号码的鞋中选四只恰有一双的情况有5×24=120种．

点评 本题考查计数原理的运用，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
10．设$\overrightarrow{a}$=（x，3），$\overrightarrow{b}$=（2，-1），根据下列条件求x的取值范围．
（1）$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角；
（2）$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为直角；
（3）$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角．
11．已知函数f（x）=$\frac{lnx}{x}$-x+$\frac{a}{x}$（a∈R）．
（1）当a=0时，求证：函数f（x）有且仅有一个极值点；
（2）若对于任意的x1，x2∈[e，+∞]且x1≠x2，有不等式$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜-1恒成立，求实数a的取值范围．
8．已知$\overrightarrow{a}$=（m-2，m+3），$\overrightarrow{b}$=（2m+1，m-2），且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是锐角，则实数m的取值范围是（　　）
A．m＞2或m＜-$\frac{4}{3}$B．-$\frac{4}{3}$＜m＜2C．m≠2D．m≠2且m≠-$\frac{4}{3}$
15．函数f（x）=$\sqrt{{x}^{2}}$是（　　）
A．偶函数B．奇函数
C．非奇非偶函数D．既是奇函数又是偶函数
5．已知f（x）=$\frac{3x+1}{{x}^{2}-1}$，求f（0），f（-2），f（a），f（x2），f（$\frac{1}{x}$）．
12．已知cosα=$\frac{\sqrt{5}}{7}$，且sinα＜0，则角α是（　　）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
9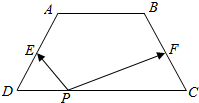．如图，在等腰梯形ABCD中，AB=2，CD=4，BC=$\sqrt{5}$，点E，F分别为AD，BC的中点．如果对于常数λ，在等腰梯形ABCD的四条边长，有且只有8个不同的点P，使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立，那么λ的取值范围是（　　）
A．（-$\frac{5}{4}$，-$\frac{9}{20}$）B．（-$\frac{9}{20}$，$\frac{11}{4}$）C．（-$\frac{9}{20}$，-$\frac{1}{4}$）D．（-$\frac{5}{4}$，$\frac{11}{4}$）
10．求定积分${∫}_{-1}^{0}$$\frac{{x}^{2}}{{x}^{2}+2x}$dx的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网