题目内容
9.(理科做)已知空间向量$\overrightarrow{a}$=(1,k,-1),$\overrightarrow{b}$=(-3,2,k),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数k的值为3.分析 令$\overrightarrow{a}$•$\overrightarrow{b}$=0,列出方程解出k.
解答 解:∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,即-3+2k-k=0,解得k=3.
故答案为3.
点评 本题考查了空间向量的数量积运算,向量垂直与数量积的关系,属于基础题.

练习册系列答案
相关题目
17.“m≥0”是“直线mx-y+1-m=0与圆(x-1)2+y2=1相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.给定空间直角坐标系中,x轴上到点P(4,1,2)的距离为$\sqrt{30}$的点有( )
| A. | 2个 | B. | 1个 | C. | 0个 | D. | 无数个 |
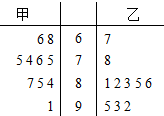 某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.
某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.