题目内容
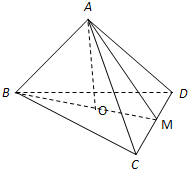 已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点.
已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点.(1)求点A到面BCD的距离;
(2)求AB与面BCD所成角的正弦值.
考点:直线与平面所成的角,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)根据棱长为a的正四面体高为
a,可求出点A到面BCD的距离,即正四面体的高;
(2)由(1)中AO的长,及AB的长,解直角三角形OAB可得AB与面BCD所成角的正弦值.
| ||
| 3 |
(2)由(1)中AO的长,及AB的长,解直角三角形OAB可得AB与面BCD所成角的正弦值.
解答:
解:(1)∵棱长为a的正四面体中
AB=BC=CD=BD=AC=AD=a
在等边三角形BCD中,CD边的上高BM=
a
过A作底面BCD上的高,则垂足O为底面BCD的重心
则BO=
BM=
a
则AO=
=
a,
∴点A到面BCD的距离OA=
a
(说明:直接由公式计算得出正确结果不扣分)…6分
(2)由(1)可得∠ABO即为AB与面BCD所成角
在Rt△OAB中,OA=
a,AB=a
∴sin∠ABO=
=
即AB与面BCD所成角的正弦值为
AB=BC=CD=BD=AC=AD=a
在等边三角形BCD中,CD边的上高BM=
| ||
| 2 |
过A作底面BCD上的高,则垂足O为底面BCD的重心
则BO=
| 2 |
| 3 |
| ||
| 3 |
则AO=
| AB2-BO2 |
| ||
| 3 |
∴点A到面BCD的距离OA=
| ||
| 3 |
(说明:直接由公式计算得出正确结果不扣分)…6分
(2)由(1)可得∠ABO即为AB与面BCD所成角
在Rt△OAB中,OA=
| ||
| 3 |
∴sin∠ABO=
| OA |
| AB |
| ||
| 3 |
即AB与面BCD所成角的正弦值为
| ||
| 3 |
点评:本题考查的知识点是直线与平面所成的角,棱锥高的公式,解答(1)的关键是熟练掌握与正四面体相关的公式,(2)的关键是构造出线面夹角的平面角

练习册系列答案
相关题目
若关于x的方程|x2-2x-3|-m+5=0有4个根,则m的取值范围为( )
| A、(0,4) |
| B、(5,9) |
| C、(0,4] |
| D、(5,9] |
若函数f(x)=x2+a|x-1|(a∈R),则对不同的实数a,函数f(x)的单调区间的个数有可能的是( )
| A、1个或2个 |
| B、2个或3个 |
| C、3个或4个 |
| D、2个或4个 |
已知二次函数f(x)=x2-(a-2)x+4是偶函数,则实数a的值为( )
| A、0 | B、4 | C、-2 | D、2 |
若直线x+y+a=0与圆(x-a)2+y2=2相切,则a=( )
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、1或-1 |