题目内容
在等比数列{an}中,已知S2=30,S4=150,则a5+a6= .
考点:等比数列的性质
专题:等差数列与等比数列
分析:由给出的数列是等比数列,得到S2,S4-S2,S6-S4也构成等比数列,由等比数列的性质列式求出S6,则a5+a6可求.
解答:
解:∵数列{an}是等比数列,S2≠0,
∴S2,S4-S2,S6-S4也构成等比数列,
∴(S4-S2)2=S2(S6-S4),
即(150-30)2=30(S6-150),
解得:S6=630.
∴S6-S4=630-150=480.
故答案为:480.
∴S2,S4-S2,S6-S4也构成等比数列,
∴(S4-S2)2=S2(S6-S4),
即(150-30)2=30(S6-150),
解得:S6=630.
∴S6-S4=630-150=480.
故答案为:480.
点评:本题考查了等比数列的性质,若数列{an}是等比数列,则Sk,S2k-Sk,S3k-S2k,…也构成等比数列,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a,b是方程x2+(cotθ)x-cosθ=0的两个不等实根,那么过点A(a,a2)和B(b,b2)的直线与圆x2+y2=1的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、随θ的值而变化 |
已知点P(x,y)的坐标x,y满足
,则x2+y2-4x的取值范围是( )
|
| A、[0,12] |
| B、[-1,12] |
| C、[3,16] |
| D、[-1,16] |
函数y=x3-x2-x的单调递增区间为( )
A、(-∞,-
| ||
B、[-
| ||
C、(-∞,-
| ||
D、[-1,
|
某几何体的三视图如图所示,则此几何体的体积是( )


A、
| ||
| B、6π | ||
C、
| ||
D、
|
 已知函数f(x)=x2-4,点A1(x1,0),过点A1作x轴的垂线交抛物线C:y=f(x)于点B1,过B1作抛物线C:y=f(x)的切线与x轴交于点A2(x2,0),过点A2作x轴的垂线交抛物线C:y=f(x)于点B2,过点B2作抛物线C:y=f(x)的切线交x轴于点A3(x3,0)┉依次下去,得到x1、x2、x3┉,xn,其中x1>0,
已知函数f(x)=x2-4,点A1(x1,0),过点A1作x轴的垂线交抛物线C:y=f(x)于点B1,过B1作抛物线C:y=f(x)的切线与x轴交于点A2(x2,0),过点A2作x轴的垂线交抛物线C:y=f(x)于点B2,过点B2作抛物线C:y=f(x)的切线交x轴于点A3(x3,0)┉依次下去,得到x1、x2、x3┉,xn,其中x1>0,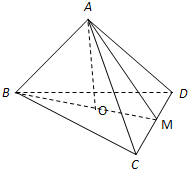 已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点.
已知正四面体ABCD的棱长为a,点O是△BCD的中心,点M是CD中点.