题目内容
若关于x的方程|x2-2x-3|-m+5=0有4个根，则m的取值范围为（ ）
| A、（0，4） |
| B、（5，9） |
| C、（0，4] |
| D、（5，9] |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由|x2-2x-3|-m+5=0得到|x2-2x-3|=m-5，然后作出函数y=|x2-2x-3|的图象，利用数形结合即可求出m 的取值范围．
解答：
解：由|x2-2x-3|-m+5=0得到|x2-2x-3|=m-5，
作出函数y=|x2-2x-3|的图象，如图：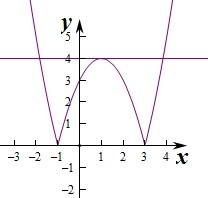
由图象可知要使|x2-2x-3|=m-5，有4个根，
则满足0＜m-5＜4，
即5＜m＜9，
故选：B．
作出函数y=|x2-2x-3|的图象，如图：
由图象可知要使|x2-2x-3|=m-5，有4个根，
则满足0＜m-5＜4，
即5＜m＜9，
故选：B．
点评：本题主要考查方程根的个数应用断，利用方程和函数之间的关系，转化为两个函数图象的交点问题是解决本题的关键，利用数形结合是解决本题的基本思想．要求熟练掌握二次函数的图象和性质．
练习册系列答案
相关题目
已知函数f（x）=x2+2bx过（1，2）点，若数列{
}的前n项和为Sn，则S2013的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a，b是方程x2+（cotθ）x-cosθ=0的两个不等实根，那么过点A（a，a2）和B（b，b2）的直线与圆x2+y2=1的位置关系是（ ）
| A、相离 | B、相切 |
| C、相交 | D、随θ的值而变化 |
若k的值使得过A（1，1）可以做两条直线与圆x2+y2+kx-2y-
k=0相切，则k的取值范围是（ ）
| 5 |
| 4 |
| A、k＜0 |
| B、k＜-4或-1＜k＜0 |
| C、k＜-4 |
| D、k＜-4或k＞-1 |
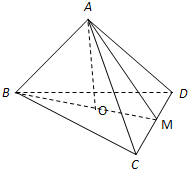已知正四面体ABCD的棱长为a，点O是△BCD的中心，点M是CD中点．