题目内容

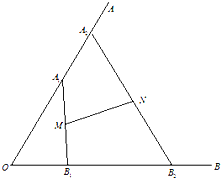如图，∠AOB=
π
3
，动点A1，A2与B1，B2分别在射线OA，OB上，且线段A1A2的长为1，线段B1B2的长为2，点M，N分别是线段A1B1，A2B2的中点．
（Ⅰ）用向量
A1A2
与
B1B2
表示向量
MN
；
（Ⅱ）求向量
MN
的模．
考点：向量在几何中的应用
专题：计算题,平面向量及应用
分析：（Ⅰ）由题意，
MN
=
MB1
+
B1B2
+
B2N
，注意到点M，N分别是线段A1B1，A2B2的中点，即可用向量
A1A2
与
B1B2
表示向量
MN
；
（Ⅱ）由已知可得向量
A1A2
与
B1B2
的模分别为1与2，夹角为
π
3
，求向量
MN
的模．
解答： 解：（Ⅰ）由题意，
MN
=
MB1
+
B1B2
+
B2N
，
注意到点M，N分别是线段A1B1，A2B2的中点，得
MN
=
1
2
(
A1A2
+
B1B2
)．…（6分）
（Ⅱ）由已知可得向量
A1A2
与
B1B2
的模分别为1与2，夹角为
π
3
，
所以
A1A2
•
B1B2
=1，
由
MN
=
1
2
(
A1A2
+
B1B2
)得|
MN
|=
1
4
(
A1A2
+
B1B2
)2
=
1
2
1+4+2×1×2×
1
2
=
7
2
…（12分）
点评：本题考查向量在几何中的应用，考查向量的加法运算，属于中档题．
练习册系列答案
相关题目
函数f（x）=
2
x-1
，其中x∈[2，5]
（1）判断函数的单调性并证明；
（2）若a＜b，且a∈[2，5]，b∈[2，5]，比较f（a）和f（b）大小，并说明理由．
an=
2n-1，(n为奇数)
2
n
2
，(n为偶数)
，则S20=
 
．
某段铁路所有车站共发行20种普通车票，那么这段铁路共有车站数是（　　）
A、4B、5C、8D、10
如图，电路中共有7个电阻与一个电灯A，若灯A不亮，分析因电阻断路的可能性共有
 
种
定义运算a?b=
a，a≤b
b，a＞b
，已知函数f（x）=x?（-x2+2），则f（x）的最大值为
 
．
直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线C1：
x=3+cost
y=4+sint
（t为参数）和曲线C2：ρ=1上，当|AB|长取得最小值时，求线段AB的垂直平分线的极坐标方程．
已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼．为了估计池塘中这两种鱼的数量，养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只，给每只鱼作上不影响其存活的记号，然后放回池塘，经过一定时间，再每次从池塘中随机地捕出1000只鱼，分类记录下其中有记号的鱼的数目，随即将它们放回池塘中．这样的记录作了10次．并将记录获取的数据做成以下的茎叶图，
（Ⅰ）根据茎叶图计算有记号的红鲫鱼与中国金鱼数目的平均数，并估计池塘中的红鲫鱼与中国金鱼的数量；
（Ⅱ）假设随机地从池塘逐只有放回地捕出5只鱼中的红鲫鱼的数目为ξ，求ξ的分布列与数学期望．
集合{a，b，c，d}的非空真子集的个数（　　）
A、16个B、15个
C、14个D、13个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网