题目内容
集合{a,b,c,d}的非空真子集的个数( )
| A、16个 | B、15个 |
| C、14个 | D、13个 |
考点:子集与真子集
专题:计算题,集合
分析:对于有限集合,我们有以下结论:若一个集合中有n个元素,则它有2n个子集.
解答:
解:∵集合{a,b,c,d}有4个元素,
∴则集合{a,b,c,d}有24=16个子集,
故集合{a,b,c,d}的非空真子集的个数为14;
故选C.
∴则集合{a,b,c,d}有24=16个子集,
故集合{a,b,c,d}的非空真子集的个数为14;
故选C.
点评:本题考查了集合的子集个数,若一个集合中有n个元素,则它有2n个子集,有(2n-1)个真子集,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
f(x)=x3+
+1,若f(a)=2,则f(-a)的值为( )
| 3 | x |
| A、3 | B、0 | C、-1 | D、-2 |
设a,b∈R,则“
>1”是“|a|>|b|”成立的( )
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
符合条件{a,b,c}⊆P⊆{a,b,c,d,e}的集合P的个数是( )
| A、2 | B、3 | C、4 | D、8 |
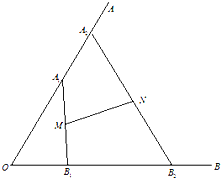 如图,∠AOB=
如图,∠AOB=