题目内容
如图,电路中共有7个电阻与一个电灯A,若灯A不亮,分析因电阻断路的可能性共有 种


考点:计数原理的应用
专题:排列组合
分析:本题通过分类研究三层电路的可能情况,再通过乘法原理,得到本题结论.
解答:
解:由灯A不亮可知:
上、中、下三层电路均不能通电.
(1)上层电路不通电,分为一个电阻不通电和两个电阻均不通电,情况有:
+
=3种;
(2)中层电路不通电,分为一个电阻不通电和两个电阻均不通电,情况有:
+
=3种;
(3)下层电路不通电,分为一个电阻不通电、两个电阻均不通电和三个电路不通电,情况有
+
+
=7种;
根据乘法原理,电阻断路的可能性共有3×3×7=63.
故答案为:63.
上、中、下三层电路均不能通电.
(1)上层电路不通电,分为一个电阻不通电和两个电阻均不通电,情况有:
| C | 1 2 |
| C | 2 2 |
(2)中层电路不通电,分为一个电阻不通电和两个电阻均不通电,情况有:
| C | 1 2 |
| C | 2 2 |
(3)下层电路不通电,分为一个电阻不通电、两个电阻均不通电和三个电路不通电,情况有
| C | 1 3 |
| C2 | 2 3 |
| C | 3 3 |
根据乘法原理,电阻断路的可能性共有3×3×7=63.
故答案为:63.
点评:本题考查了排列组合的知识和分类讨论的数学思想,本题难度不大,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知函数f(x)是R上的可导函数,f(x)的导数f′(x)的图象如图,则下列结论正确的是( )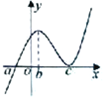

| A、a,c分别是极大值点和极小值点 |
| B、b,c分别是极大值点和极小值点 |
| C、f(x)在区间(a,c)上是增函数 |
| D、f(x)在区间(b,c)上是减函数 |
函数y=|x-1|的图象为( )
A、 |
B、 |
C、 |
D、 |
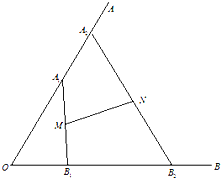 如图,∠AOB=
如图,∠AOB= 如图所示,图中有5组数据,去掉
如图所示,图中有5组数据,去掉