题目内容
an=
，则S20= ．
|
考点：数列的求和
专题：等差数列与等比数列
分析：本题可以将原数列转化为一个等差数列和一个等比数列，再分别求它们的和，相加后，得到本题结论．
解答：
解：∵an=
，
∴奇数项依次为：
a1=1，a3=5，a5=9，…构成一个等差数列，首项为1，公差为4．
偶数项依次为：
a2=21=2，a4=22=4，a6=23=8，…构成一个等比数列，首项为2，公比为2．
∴S20=a1+a2+a3+a4+…+a20
=（a1+a3+…+a19）+（a2+a4+…+a20）
=10×1+
×4+
=2236．
故答案为2236．
|
∴奇数项依次为：
a1=1，a3=5，a5=9，…构成一个等差数列，首项为1，公差为4．
偶数项依次为：
a2=21=2，a4=22=4，a6=23=8，…构成一个等比数列，首项为2，公比为2．
∴S20=a1+a2+a3+a4+…+a20
=（a1+a3+…+a19）+（a2+a4+…+a20）
=10×1+
| 10×9 |
| 2 |
| 2(1-210) |
| 1-2 |
=2236．
故答案为2236．
点评：本题考查的数列求和的知识，用到了转化求和的方法，考查了化归转化的数学思想，本题难度不大，属于基础题．
练习册系列答案
一课一练课时达标系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
给出下列函数①f（x）=（
）x；②f（x）=x2；③f（x）=sinx，x∈（-
，0）；④f（x）=x
；⑤f（x）=log2x．其中满足条件f （
）＞
（0＜x1＜x2）的函数的个数是（ ）
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知四边形ABCD是边长为1的正方形，MA⊥平面ABCD，MA=2动点P在正方形的边上从点A出发经过点B运动到点C．设点P走过的路程为x，△MAP的面积为S（x），则函数y=S2（x）的图象是（ ）
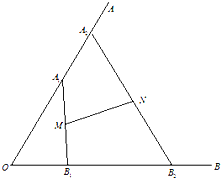如图，∠AOB=