题目内容
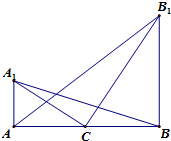如图，在水平地面上有两座直立的相距60m的铁塔AA1和BB1．已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍，从两塔底部连线中点C分别看两塔顶部的仰角互为余角．则从塔BB1的底部看塔AA1顶部的仰角的正切值为考点：解三角形的实际应用
专题：应用题,解三角形
分析：设从塔BB1的底部看塔AA1顶部的仰角为α，则AA1=60tanα，BB1=60tan2α，利用从两塔底部连线中点C分别看两塔顶部的仰角互为余角，可得△A1AC∽△CBB1，即可求出结论．
解答：
解：设从塔BB1的底部看塔AA1顶部的仰角为α，则AA1=60tanα，BB1=60tan2α，
∵从两塔底部连线中点C分别看两塔顶部的仰角互为余角，
∴△A1AC∽△CBB1，
∴
=
，
∴AA1•BB1=900，
∴3600tanαtan2α=900，
∴tanα=
，tan2α=
，BB1=60tan2α=45．
故答案为：
，45
∵从两塔底部连线中点C分别看两塔顶部的仰角互为余角，
∴△A1AC∽△CBB1，
∴
| AA1 |
| 30 |
| 30 |
| BB1 |
∴AA1•BB1=900，
∴3600tanαtan2α=900，
∴tanα=
| 1 |
| 3 |
| 3 |
| 4 |
故答案为：
| 1 |
| 3 |
点评：本题考查解三角形的实际应用，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=
（0＜φ＜
）的图象如图，则（ ）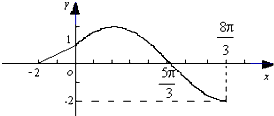
|
| π |
| 2 |
A、k=
| ||||||
B、k=
| ||||||
C、k=-
| ||||||
D、k=-2，ω=2，φ=
|