题目内容
符号[x]表示不超过x的最大整数,如[π]=3,[-1.8]=-2,定义函数:f(x)=x-[x],则下列命题正确的序号是 .
①f(-0.2)=0.8;
②方程f(x)=
有无数个解;
③函数f(x)是增函数;
④函数f(x)是奇函数;
⑤函数f(x)的定义域为R,值域为[0,1].
①f(-0.2)=0.8;
②方程f(x)=
| 1 |
| 2 |
③函数f(x)是增函数;
④函数f(x)是奇函数;
⑤函数f(x)的定义域为R,值域为[0,1].
考点:命题的真假判断与应用
专题:函数的性质及应用,推理和证明
分析:由符号[x]表示不超过x的最大整数,f(x)=x-[x],可以画出其图象根据图象就比较容易判断了.
解答:
解:作出函数f(x)=x-[x]的图象,如同所示
对于①结论三正确的,∵[x]表示不超过x的最大整数,∴[-0.2]=-1,∴f(-0.2)=-0.2-(-1)=0.8.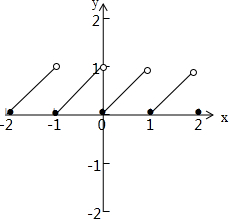
对于②结论是正确的,可以看出函数是周期函数,故方程有无数解是正确的.
③是不正确的,因为函数是周期函数,所以不是递增函数.
④是不正确的,取特殊值,∵f(-0.5)=f(0.5)=0.5,∴④是不正确的.
⑤由图象可知,结论三不正确的,值域是[0,1),∴⑤是不正确的.
故答案为:①②
对于①结论三正确的,∵[x]表示不超过x的最大整数,∴[-0.2]=-1,∴f(-0.2)=-0.2-(-1)=0.8.

对于②结论是正确的,可以看出函数是周期函数,故方程有无数解是正确的.
③是不正确的,因为函数是周期函数,所以不是递增函数.
④是不正确的,取特殊值,∵f(-0.5)=f(0.5)=0.5,∴④是不正确的.
⑤由图象可知,结论三不正确的,值域是[0,1),∴⑤是不正确的.
故答案为:①②
点评:本题考查新函数的定义,函数性质的判断,所以基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
函数f(x)=lnx-3+x的零点为x1,g(x)=ex-3+x的零点为x2,则x1+x2等于( )
| A、2 | B、3 | C、6 | D、1 |
若存在对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上均有零点,则称x0为函数f(x)的一个“纽点”.则下列四个函数中,不存在“纽点”的是( )
| A、f(x)=x2+bx-1(b∈R) | ||
| B、f(x)=2x-x2 | ||
C、f(x)=
| ||
| D、f(x)=2-|x-1| |
已知A,B,C是圆O:x2+y2=1上任意的不同三点,若
=3
+x
,则正实数x的取值范围为( )
| OA |
| OB |
| OC |
| A、(0,2) |
| B、(2,4) |
| C、(1,4) |
| D、(2,3) |
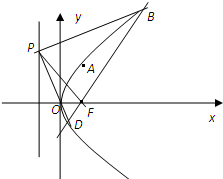 在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.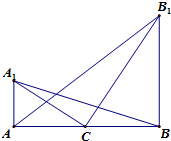 如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为
如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为