题目内容
在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinB=2sin(
+B)•sin(
-B).
(Ⅰ)求角B的大小;
(Ⅱ)若b=1,求△ABC的面积的最大值.
| π |
| 4 |
| π |
| 4 |
(Ⅰ)求角B的大小;
(Ⅱ)若b=1,求△ABC的面积的最大值.
考点:两角和与差的正弦函数,正弦定理
专题:三角函数的求值,解三角形
分析:(Ⅰ)利用两角和与差的正弦公式化简式子,利用平方关系、条件求出角B的值;
(Ⅱ)利用余弦定理得:b2=a2+c2-2accosB,把数据代入利用不等式求出ac的范围,代入三角形的面积公式求出面积的最大值.
(Ⅱ)利用余弦定理得:b2=a2+c2-2accosB,把数据代入利用不等式求出ac的范围,代入三角形的面积公式求出面积的最大值.
解答:
解:(Ⅰ)由条件得sinB=2(
cosB+
sinB)(
cosB-
sinB),
即sinB=cos2B-sin2B,
由sin2B+cos2B=1得,2sin2B+sinB-1=0,
解得sinB=
或sinB=-1…(5分)
因为△ABC是锐角三角形,所以B=
…(7分)
(Ⅱ)由余弦定理:b2=a2+c2-2accosB,
把b=1,B=
代入可以得到:
1=a2+c2-
ac≥(2-
)ac,所以ac≤
=2+
…(10分)
所以S△ABC=
acsinB=
ac≤
…(13分)
当且仅当a=c时取等号,此时△ABC的面积的最大值是
…(14分)
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
即sinB=cos2B-sin2B,
由sin2B+cos2B=1得,2sin2B+sinB-1=0,
解得sinB=
| 1 |
| 2 |
因为△ABC是锐角三角形,所以B=
| π |
| 6 |
(Ⅱ)由余弦定理:b2=a2+c2-2accosB,
把b=1,B=
| π |
| 6 |
1=a2+c2-
| 3 |
| 3 |
| 1 | ||
2-
|
| 3 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
2+
| ||
| 4 |
当且仅当a=c时取等号,此时△ABC的面积的最大值是
2+
| ||
| 4 |
点评:本题考查两角和与差的正弦公式,余弦定理,平方关系等,以及利用不等式求三角形面积的最大值,这是常考的题型.

练习册系列答案
相关题目
已知A,B,C是圆O:x2+y2=1上任意的不同三点,若
=3
+x
,则正实数x的取值范围为( )
| OA |
| OB |
| OC |
| A、(0,2) |
| B、(2,4) |
| C、(1,4) |
| D、(2,3) |
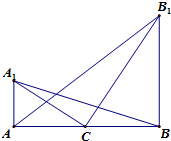 如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为
如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为