题目内容
已知函数f(x)=
在x=1处取得极值2.
(1)求函数f(x)的表达式;
(2)若函数f(x)在区间(m,2m+1)上单调递增,求实数m的取值范围;
(3)若直线l与f(x)的图象相切,求直线l的斜率k的取值范围.
| ax |
| x2+b |
(1)求函数f(x)的表达式;
(2)若函数f(x)在区间(m,2m+1)上单调递增,求实数m的取值范围;
(3)若直线l与f(x)的图象相切,求直线l的斜率k的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)由题意对函数求导,然后利用极值的概念列出a,b的方程,在求解即可;
(2)由题意应该先求具体函数的单调区间,然后利用已知的条件及集合的思想,建立的m取值范围的不等式組求解即可;
(3)由条件知,过f(x)的图形上一点P(x0,y0)的切线l的斜率k为:k=4[
-
],换元进而可求直线l的斜率k的取值范围.
(2)由题意应该先求具体函数的单调区间,然后利用已知的条件及集合的思想,建立的m取值范围的不等式組求解即可;
(3)由条件知,过f(x)的图形上一点P(x0,y0)的切线l的斜率k为:k=4[
| 2 |
| (1+x02)2 |
| 1 |
| 1+x02 |
解答:
解:(1)求导,f′(x)=
,
又f(x)在x=1处取得极值2,
所以
,
解得a=4,b=1
所以f(x)=
.
(2)因为f′(x)=
,
又f(x)的定义域是R,所以由f'(x)>0,
得-1<x<1.所以f(x)在[-1,1]上单调递增,
在(-∞,-1]和[1,+∞)上单调递减.
①当f(x)在区间(m,2m+1)上单调递增,
则
,解得-1<m≤0;
②当f(x)在区间(m,2m+1)上单调递减,
则
或
,解得m≥1.
综上,实数m的取值范围是-1<m≤0或m≥1.
(3)f′(x)=
由条件知,过f(x)的图形上一点P(x0,y0)的切线l的斜率k为:k=4[
-
]
令t=
,则t∈(0,1]
此时,k=8(t-
)2-
根据二次函数的图象性质知:当t=
时,kmin=-
,
当t=1时,kmax=4.
所以,直线l的斜率k的取值范围是[-
,4].
| a(-x2+b) |
| (x2+b)2 |
又f(x)在x=1处取得极值2,
所以
|
解得a=4,b=1
所以f(x)=
| 4x |
| x2+1 |
(2)因为f′(x)=
| -4(x+1)(x-1) |
| (x2+1)2 |
又f(x)的定义域是R,所以由f'(x)>0,
得-1<x<1.所以f(x)在[-1,1]上单调递增,
在(-∞,-1]和[1,+∞)上单调递减.
①当f(x)在区间(m,2m+1)上单调递增,
则
|
②当f(x)在区间(m,2m+1)上单调递减,
则
|
|
综上,实数m的取值范围是-1<m≤0或m≥1.
(3)f′(x)=
| -4(x+1)(x-1) |
| (x2+1)2 |
由条件知,过f(x)的图形上一点P(x0,y0)的切线l的斜率k为:k=4[
| 2 |
| (1+x02)2 |
| 1 |
| 1+x02 |
令t=
| 1 |
| 1+x02 |
此时,k=8(t-
| 1 |
| 4 |
| 1 |
| 2 |
根据二次函数的图象性质知:当t=
| 1 |
| 4 |
| 1 |
| 2 |
当t=1时,kmax=4.
所以,直线l的斜率k的取值范围是[-
| 1 |
| 2 |
点评:本题以函数为载体,考查导数的运用,考查函数的极值,考查函数的单调性,同时考查了导数的几何意义,还考查了数学中常用的分类讨论的思想.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若存在对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上均有零点,则称x0为函数f(x)的一个“纽点”.则下列四个函数中,不存在“纽点”的是( )
| A、f(x)=x2+bx-1(b∈R) | ||
| B、f(x)=2x-x2 | ||
C、f(x)=
| ||
| D、f(x)=2-|x-1| |
如果如图撑血运行后,输出结果为132,那么程序中UNTIL,后面的条件应为( )


| A、i>11 | B、i≥11 |
| C、i≤11 | D、i<11 |
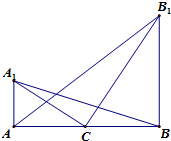 如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为
如图,在水平地面上有两座直立的相距60m的铁塔AA1和BB1.已知从塔AA1的底部看塔BB1顶部的仰角是从塔BB1的底部看塔AA1顶部的仰角的2倍,从两塔底部连线中点C分别看两塔顶部的仰角互为余角.则从塔BB1的底部看塔AA1顶部的仰角的正切值为