题目内容
方程ax2+2x+1=0恰有一个负实根,则a的取值范围为( )
| A、a<0 | B、a≤0 |
| C、a>0 | D、a=0 |
考点:一元二次方程的根的分布与系数的关系
专题:综合题,不等式的解法及应用
分析:方程ax2+2x+1=0为一个类二次方程,故我们要分a=0和a≠0两种情况进行讨论,当a=0时方程为一次方程,可直接求解进行判断,当a≠0时,方程为二次方程,可利用韦达定理进行判断.
解答:
解:①当a=0时,原方程可化为2x+1=0,解得x=-
;
②当a>0时,由韦达定理得-
<0,
>0,此时方程有两个负数根,不满足题意;
③当a<0时,由韦达定理得-
>0,
<0,此时方程有一个正数根,一个负数根,满足题意
∴a≤0.
故选B.
| 1 |
| 2 |
②当a>0时,由韦达定理得-
| 2 |
| a |
| 1 |
| a |
③当a<0时,由韦达定理得-
| 2 |
| a |
| 1 |
| a |
∴a≤0.
故选B.
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,其中本题易忽略对a=0的讨论,另外熟练掌握是韦达定理是解答本题的关键.

练习册系列答案
相关题目
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测n(n∈N+)个平面最多将空间分成( )
| A、2n部分 | ||
| B、n2部分 | ||
| C、2n部分 | ||
D、
|
直线
x-3y+2=0和直线
x+y-1=0的倾斜角分别为α,β,tan(α+β)=( )
| 3 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
直线l:y=kx+4-2k与曲线y=1+
有两个交点时,实数k的取值范围是( )
| 4-x2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
sin(-585°)的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
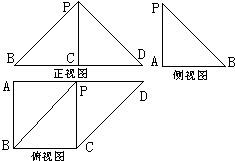 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )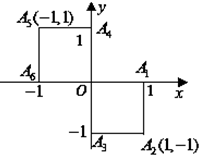 小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.