题目内容
已知函数f(x)＝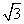
sin2x＋2cos2x.
(1)将f(x)的图象向右平移π/12个单位长度，再将周期扩大一倍，得到函数g(x)的图象，求g(x)的解析式；
(2)求函数f(x)的最小正周期和单调递增区间．
解析 (1)依题意f(x)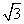＝sin2x＋2·
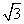＝sin2x＋cos2x＋1
＝2sin
＋1，
将f(x)的图象向右平移
个单位长度，得到函数f1(x)＝2sin
＋1＝2sin2x＋1的图象，该函数的周期为π，若将其周期变为2π，则得g(x)＝2sinx＋1.
(2)函数f(x)的最小正周期为T＝π，
当
(k∈Z)时，函数单调递增，
解得
(k∈Z)，
∴函数的单调递增区间为
(k∈Z)．
练习册系列答案
名校通行证有效作业系列答案
相关题目
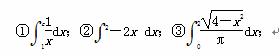④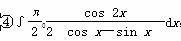
，积分值等于1的个数是( )．
＋1)x＋m＝0的两根sin θ和cos θ，θ∈(0,2π)，求：
＋
的值；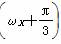
(ω>0)的最小正周期为π，则该函数的图象( )
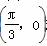对称 B．关于直线x＝
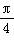对称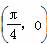
对称 D．关于直线x＝
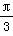对称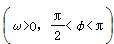
的图象，向右最少平移
个单位长度，或向左最少平移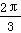
个单位长度，所得到的函数图象均关于原点中心对称，则ω＝________.
，则sin 2α等于( )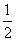
B．－
D．－
