题目内容
已知函数f(x)满足f(x•y)=f(x)+f(y)且f(2)=a,f(3)=b,求f(108).
考点:抽象函数及其应用
专题:函数的性质及应用
分析:利用已知条件,分解108为4×9×3,利用条件求解即可.
解答:
解:f(x•y)=f(x)+f(y),f(2)=a,f(3)=b,
∵108=36×3=4×9×3.
∴f(108)=f(36×3)
=f(36)+f(3)
=f(4×9)+f(3)
=2f(2)+3f(3)
=2a+3b.
∴f(108)=2a+3b.
∵108=36×3=4×9×3.
∴f(108)=f(36×3)
=f(36)+f(3)
=f(4×9)+f(3)
=2f(2)+3f(3)
=2a+3b.
∴f(108)=2a+3b.
点评:本题考查函数值的求法,抽象函数的应用,考查计算能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” |
| B、“x=-1”是“x2-2x+3=0”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
y=f(x)是定义在R上的函数,若a∈R,则“x≠a”是“f(x)≠f(a)”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
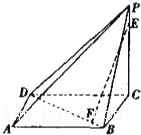 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.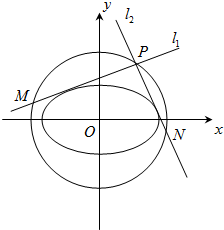 给定椭圆C:
给定椭圆C: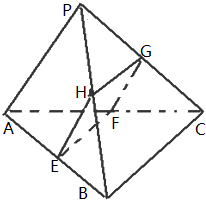 如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)
如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)