题目内容
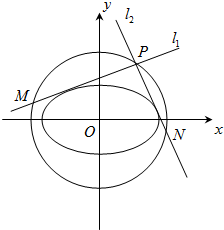 给定椭圆C:
给定椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1,l2交“准圆”于点M,N.
(ⅰ)当点P为“准圆”与y轴正半轴的交点时,求直线l1,l2的方程并证明l1⊥l2;
(ⅱ)求证:线段MN的长为定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)利用已知椭圆的标准方程及其b=
即可得出;
(Ⅱ)(i)把直线方程代入椭圆方程转化为关于x的一元二次方程,利用直线与椭圆相切?△=0,即可解得k的值,进而利用垂直与斜率的关系即可证明;
(ii)分类讨论:l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,无论两条直线中的斜率是否存在,都有l1,l2垂直.即可得出线段MN为准圆x2+y2=4的直径.
| a2-c2 |
(Ⅱ)(i)把直线方程代入椭圆方程转化为关于x的一元二次方程,利用直线与椭圆相切?△=0,即可解得k的值,进而利用垂直与斜率的关系即可证明;
(ii)分类讨论:l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,无论两条直线中的斜率是否存在,都有l1,l2垂直.即可得出线段MN为准圆x2+y2=4的直径.
解答:
(Ⅰ)解:∵椭圆C的一个焦点为F(
,0),其短轴上的一个端点到F的距离为
.
∴c=
,a=
,
∴b=
=1,
∴椭圆方程为
+y2=1,
∴准圆方程为x2+y2=4.
(Ⅱ)证明:(ⅰ)∵准圆x2+y2=4与y轴正半轴的交点为P(0,2),
设过点P(0,2)且与椭圆相切的直线为y=kx+2,
联立
得(1+3k2)x2+12kx+9=0.
∵直线y=kx+2与椭圆相切,
∴△=144k2-4×9(1+3k2)=0,解得k=±1,
∴l1,l2方程为y=x+2,y=-x+2.
∵kl1•kl2=-1,
∴l1⊥l2.
(ⅱ)①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,
则l1:x=±
,
当l1:x=
时,l1与准圆交于点(
,1),(
,-1),
此时l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证当l1:x=-
时,直线l1,l2垂直.
②当l1,l2斜率存在时,设点P(x0,y0),其中
+
=4.
设经过点P(x0,y0)与椭圆相切的直线为y=t(x-x0)+y0,
∴由
得 (1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由△=0化简整理得 (3-
)t2+2x0y0t+1-
=0,
∵
+
=4,∴有(3-
)t2+2x0y0t+(
-3)=0.
设l1,l2的斜率分别为t1,t2,
∵l1,l2与椭圆相切,
∴t1,t2满足上述方程(3-
)t2+2x0y0t+(
-3)=0,
∴t1•t2=-1,即l1,l2垂直.
综合①②知:∵l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直.
∴线段MN为准圆x2+y2=4的直径,|MN|=4,
∴线段MN的长为定值.
| 2 |
| 3 |
∴c=
| 2 |
| 3 |
∴b=
| a2-c2 |
∴椭圆方程为
| x2 |
| 3 |
∴准圆方程为x2+y2=4.
(Ⅱ)证明:(ⅰ)∵准圆x2+y2=4与y轴正半轴的交点为P(0,2),
设过点P(0,2)且与椭圆相切的直线为y=kx+2,
联立
|
∵直线y=kx+2与椭圆相切,
∴△=144k2-4×9(1+3k2)=0,解得k=±1,
∴l1,l2方程为y=x+2,y=-x+2.
∵kl1•kl2=-1,
∴l1⊥l2.
(ⅱ)①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,
则l1:x=±
| 3 |
当l1:x=
| 3 |
| 3 |
| 3 |
此时l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证当l1:x=-
| 3 |
②当l1,l2斜率存在时,设点P(x0,y0),其中
| x | 2 0 |
| y | 2 0 |
设经过点P(x0,y0)与椭圆相切的直线为y=t(x-x0)+y0,
∴由
|
得 (1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由△=0化简整理得 (3-
| x | 2 0 |
| y | 2 0 |
∵
| x | 2 0 |
| y | 2 0 |
| x | 2 0 |
| x | 2 0 |
设l1,l2的斜率分别为t1,t2,
∵l1,l2与椭圆相切,
∴t1,t2满足上述方程(3-
| x | 2 0 |
| x | 2 0 |
∴t1•t2=-1,即l1,l2垂直.
综合①②知:∵l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直.
∴线段MN为准圆x2+y2=4的直径,|MN|=4,
∴线段MN的长为定值.
点评:本题考查了椭圆的标准方程及其性质、新定义、直线与椭圆相切?△=0、直线垂直与斜率的关系、分类讨论等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
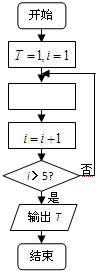 如图所示的程序框图,若执行的运算是1×
如图所示的程序框图,若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•(i+1) | ||
C、T=T•
| ||
D、T=T•
|
 已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.