题目内容
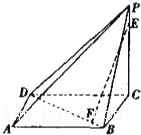 已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.
已知四棱锥P-ABCD中,PC⊥底面ABCD,PC=2,且底面ABCD是边长为1的正方形.E是最短的侧棱PC上的动点.(Ⅰ)求证:P、A、B、C、D五点在同一个球面上,并求该球的体积;
(Ⅱ)如果点F在线段BD上,DF=3BF,EF∥平面PAB,求
| PE |
| EC |
考点:与二面角有关的立体几何综合题,球的体积和表面积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)设PA的中点为M,证明CM=PM=AM=BM=DM,即可得出结论;
(Ⅱ)连接CF并延长交AB于K,连接PK,则利用线面平行的性质,可得EF∥PK,利用DF=3BF,AB∥CD,即可得出结论.
(Ⅱ)连接CF并延长交AB于K,连接PK,则利用线面平行的性质,可得EF∥PK,利用DF=3BF,AB∥CD,即可得出结论.
解答:
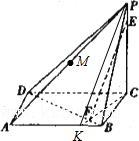 (Ⅰ)证明:设PA的中点为M,则
(Ⅰ)证明:设PA的中点为M,则
∵△PAC为直角三角形,
∴CM=PM=AM=
.
设正方形ABCD的中心为点O,则OM∥PC,OM=1且PC⊥底面ABCD,
∴OM⊥底面ABCD,
∵O为BD的中点,
∴BM=DM=
,
∴CM=PM=AM=BM=DM,
∴P、A、B、C、D五点在以M为球心,半径为
的同一个球面上,球的体积为
π•(
)3=
π;
(Ⅱ)解:连接CF并延长交AB于K,连接PK,则
∵EF∥平面PAB,EF?面PCK,面PCK∩平面PAB=PK,
∴EF∥PK,
∵DF=3BF,AB∥CD,
∴CF=3KF,
∵EF∥PK,
∴CE=3PE,
∴
=
.
 (Ⅰ)证明:设PA的中点为M,则
(Ⅰ)证明:设PA的中点为M,则∵△PAC为直角三角形,
∴CM=PM=AM=
| ||
| 2 |
设正方形ABCD的中心为点O,则OM∥PC,OM=1且PC⊥底面ABCD,
∴OM⊥底面ABCD,
∵O为BD的中点,
∴BM=DM=
| ||
| 2 |
∴CM=PM=AM=BM=DM,
∴P、A、B、C、D五点在以M为球心,半径为
| ||
| 2 |
| 4 |
| 3 |
| ||
| 2 |
| 6 |
(Ⅱ)解:连接CF并延长交AB于K,连接PK,则
∵EF∥平面PAB,EF?面PCK,面PCK∩平面PAB=PK,
∴EF∥PK,
∵DF=3BF,AB∥CD,
∴CF=3KF,
∵EF∥PK,
∴CE=3PE,
∴
| PE |
| EC |
| 1 |
| 3 |
点评:本题考查线面平行的性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设a=log3
,b=log0.62,c=
,则( )
| 1 |
| 2 |
| 3 | 3 |
| A、b<a<c |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
 已知直线x-2y+2=0经过椭圆C:
已知直线x-2y+2=0经过椭圆C: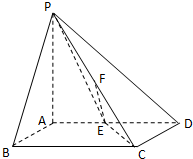 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点. 已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.