题目内容
已知函数f(x)=a(x-
)-lnx,
(1)若f(x)在定义域内为增函数,求a的取值范围;
(2)在(1)的条件下,设函数g(x)=
,若在[1,e]上至少存在一个x0,使得f(x0)≥g(x0)成立,求实数a的取值范围.
| 1 |
| x |
(1)若f(x)在定义域内为增函数,求a的取值范围;
(2)在(1)的条件下,设函数g(x)=
| e |
| x |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(1)求导函数,利用f(x)在定义域内为增函数,可得f′(x)=a+a•
-
0在(0,+∞)上恒成立,分离参数,求出右边的最大值,即可求a的取值范围;
(2)在[1,e]上至少存在一个x0,使得f(x0)≥g(x0)成立,等价于f(x)max≥g(x)min,可得f(e)≥g(e),即可求出实数a的取值范围.
| 1 |
| x2 |
| 1 |
| x |
(2)在[1,e]上至少存在一个x0,使得f(x0)≥g(x0)成立,等价于f(x)max≥g(x)min,可得f(e)≥g(e),即可求出实数a的取值范围.
解答:
解:(1)∵函数f(x)=a(x-
)-lnx,
∴f′(x)=a+a•
-
,
∵f(x)在定义域内为增函数,
∴f′(x)=a+a•
-
≥0在(0,+∞)上恒成立,
∴a≥
在(0,+∞)上恒成立,
∵x+
≥2,
∴0<
≤
,
∴a≥
;
(2)在[1,e]上至少存在一个x0,使得f(x0)≥g(x0)成立,等价于f(x)max≥g(x)min,
∴f(e)≥g(e),
∴a(e-
)-lne≥1,
∴a≥
.
| 1 |
| x |
∴f′(x)=a+a•
| 1 |
| x2 |
| 1 |
| x |
∵f(x)在定义域内为增函数,
∴f′(x)=a+a•
| 1 |
| x2 |
| 1 |
| x |
∴a≥
| 1 | ||
x+
|
∵x+
| 1 |
| x |
∴0<
| 1 | ||
x+
|
| 1 |
| 2 |
∴a≥
| 1 |
| 2 |
(2)在[1,e]上至少存在一个x0,使得f(x0)≥g(x0)成立,等价于f(x)max≥g(x)min,
∴f(e)≥g(e),
∴a(e-
| 1 |
| e |
∴a≥
| 2e |
| e2-1 |
点评:本题考查导数知识的运用,考查恒成立问题,考查函数的最大值,考查小时分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合A={x|2x-1>0},B={x||x|<1},则A∩B=( )
A、{
| ||
| B、(-1,1) | ||
C、[-1,
| ||
D、(
|
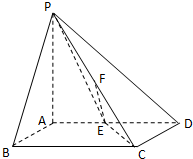 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点. 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线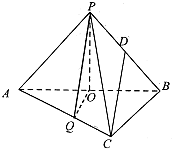 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.