题目内容
下列有关命题的说法正确的是( )
| A、命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” |
| B、“x=-1”是“x2-2x+3=0”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
考点:命题的真假判断与应用,四种命题,充要条件,命题的否定
专题:阅读型,简易逻辑
分析:根据四种命题的定义,写出原命题的否命题,可判断A的真假;根据充要条件的定义,分析“x=-1”与“x2-5x-6=0”的关系,可判断B的真假;根据特称命题的否定方法,可以判断C的真假;根据同角或等角的三角函数相等,可判断D的真假;进而得到答案
解答:
解:命题“若x2>1,则x>1”的否命题为:“若x2≤1,则x≤1”,故A错误;
“x=-1”是“x2-2x+3=0”的既不充分又不必要条件,故B错误;
命题“?x∈R,x2+x+1<0”的否定是:“?x∈R,x2+x+1≥0”,故C错误;
若x=y,则x与y的各三角函数值相等,再由逆否命题与原命题等价,故D正确;
故选D.
“x=-1”是“x2-2x+3=0”的既不充分又不必要条件,故B错误;
命题“?x∈R,x2+x+1<0”的否定是:“?x∈R,x2+x+1≥0”,故C错误;
若x=y,则x与y的各三角函数值相等,再由逆否命题与原命题等价,故D正确;
故选D.
点评:本题考查的知识点是四种命题,充要条件,全(特)称命题的否定,三角函数的定义,判断时注意命题的否定与否命题的区别,熟练掌握这些基础知识点,并利用这些基础知识判断各个命题的真假是解答本题的关键.

练习册系列答案
相关题目
若集合A={x|2x-1>0},B={x||x|<1},则A∩B=( )
A、{
| ||
| B、(-1,1) | ||
C、[-1,
| ||
D、(
|
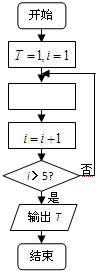 如图所示的程序框图,若执行的运算是1×
如图所示的程序框图,若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•(i+1) | ||
C、T=T•
| ||
D、T=T•
|
 已知直线x-2y+2=0经过椭圆C:
已知直线x-2y+2=0经过椭圆C: 已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.