题目内容
y=f（x）是定义在R上的函数，若a∈R，则“x≠a”是“f（x）≠f（a）”成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据逆否命题的等价性，判断f（x）=f（a）与x=a的关系即可得到结论．
解答：
解：若f（x）=f（a），则x=a不一定成立，比如函数f（x）=|x|，若f（x）=f（a），则|x|=|a|，则x=a或x=-a，（a＞0），
如x=a，则f（x）=f（a），
则f（x）=f（a）是x=a成立的必要不充分条件，
根据逆否命题的等价性可知“x≠a”是“f（x）≠f（a）”成立的必要不充分条件，
故选：B
如x=a，则f（x）=f（a），
则f（x）=f（a）是x=a成立的必要不充分条件，
根据逆否命题的等价性可知“x≠a”是“f（x）≠f（a）”成立的必要不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，利用逆否命题的等价性是解决本题的关键．
练习册系列答案
相关题目
若集合A={x|2x-1＞0}，B={x||x|＜1}，则A∩B=（ ）
A、{
| ||
| B、（-1，1） | ||
C、[-1，
| ||
D、（
|
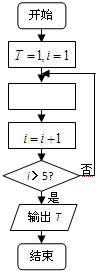如图所示的程序框图，若执行的运算是1×| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•i | ||
| B、T=T•（i+1） | ||
C、T=T•
| ||
D、T=T•
|
如图，在平面直角坐标系中，直线y=kx+b（k≠0）分别交双曲线