题目内容
17.函数f(x)=Asin(ωx+φ)的单调递减区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z),则下列说法错误的是( )| A. | 函数f(-x)的最小正周期为π | |
| B. | 函数f(-x)图象的对称轴方程为x=$\frac{π}{12}$+$\frac{kπ}{2}$(k∈Z) | |
| C. | 函数f(-x)图象的对称中心为($\frac{π}{6}$+$\frac{kπ}{2}$,0)(k∈Z) | |
| D. | 函数f(-x)的单调递减区间为[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) |
分析 由题意,ω=2,函数f(x)=Asin(ωx+φ)的周期为π,φ=$\frac{2π}{3}$,f(-x)=Asin(-2x+$\frac{2π}{3}$),再进行验证,即可得出结论.
解答 解:由题意,ω=2,函数f(x)=Asin(ωx+φ)的周期为π,
φ=$\frac{2π}{3}$,f(-x)=Asin(-2x+$\frac{2π}{3}$),
x=$\frac{π}{6}$+$\frac{kπ}{2}$,-2x+$\frac{2π}{3}$=kπ+$\frac{π}{3}$,f(-x)=Asin(-2x+$\frac{2π}{3}$)≠0,
故选C.
点评 本题考查三角函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
8.已知O为原点,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)上的点P作两条渐近线的平行线,且与两渐近线的交点分别为A,B,平行四边形OBPA的面积为2,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
5.一次函数y=-$\frac{m}{n}$x+$\frac{1}{n}$的图象同时经过第一、二、四象限的必要不充分条件是( )
| A. | mn>0 | B. | m>1,且n>1 | C. | m>0,且n<0 | D. | m>0,且n>0 |
12.sin80°cos70°+sin10°sin70°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.直线$\sqrt{3}$x-y+3=0的倾斜角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 150° |
6.已知sin(π+α)=$\frac{1}{2}$,则cos(α-$\frac{3}{2}$π)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
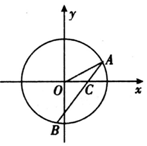 如图所示,已知A,B是单位圆上两点且|AB|=$\sqrt{3}$,设AB与x轴正半轴交于点C,α=∠AOC,β=∠OCB,则sinαsinβ+cosαcosβ=$\frac{\sqrt{3}}{2}$.
如图所示,已知A,B是单位圆上两点且|AB|=$\sqrt{3}$,设AB与x轴正半轴交于点C,α=∠AOC,β=∠OCB,则sinαsinβ+cosαcosβ=$\frac{\sqrt{3}}{2}$.