题目内容
20.某班有6名班干部,其中男生4人,女生2人,任选3人参加学校组织的义务植树活动.(I) 求男生甲、女生乙至少有1人被选中的概率;
(II) 设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P (A)和P (B|A).
分析 (1)利用对立事件的概率公式求解即可;
(2)求出男生甲被选中的概率、男生甲、女生乙都被选中的概率,即可得出结论.
解答 解:(1)男生甲、女生乙至少有1人被选中的概率P=1-$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{4}{5}$;
(2)P(A)=$\frac{{C}_{5}^{2}}{{C}_{6}^{3}}$=$\frac{1}{2}$,P(AB)=$\frac{{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$,P(B|A)=$\frac{\frac{1}{5}}{\frac{1}{2}}$=$\frac{2}{5}$.
点评 本题考查随机事件的概率和条件概率公式等知识,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.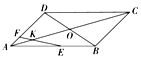 如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
 如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{10}{27}$ | D. | $\frac{11}{27}$ |
10.下列说法错误的是( )
| A. | 若命题p∧q为假命题,则p,q都是假命题 | |
| B. | 已知命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,x02+x0+1≤0 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆命题为:“若x≠1,则x2-3x+2≠0” | |
| D. | “x=1”是“x2-3x+2=0”的充分不必要条件 |