题目内容
4．己知数列{an}是等比数列，b1009是1和3的等差中项，则b1b2017=（ ）| A． | 16 | B． | 8 | C． | 2 | D． | 4 |
分析 由等差中项求出b1009=2，由此利用等比数列通项公式能求出b1b2017=${{b}_{1009}}^{2}$的值．
解答 解：∵数列{an}是等比数列，b1009是1和3的等差中项，
∴b1009=$\frac{1+3}{2}$=2，
b1b2017=${{b}_{1009}}^{2}$=4．
故选：D．
点评 本题考查等比数列的两项积的求法，是基础题，解题时要认真审题，注意等比数列、等差中项的性质的合理运用．
练习册系列答案
相关题目
14．设[x]表示不小于实数x的最小整数，如[2.6]=3，[-3.5]=-3．已知函数f（x）=[x]2-2[x]，若函数F（x）=f（x）-k（x-2）+2在（-1，4]上有2个零点，则k的取值范围是（ ）
| A． | $[{-\frac{5}{2}，-1}）∪[2，5）$ | B． | $[{-1，-\frac{2}{3}}）∪[5，10）$ | C． | $（{-\frac{4}{3}，-1}]∪[5，10）$ | D． | $[{-\frac{4}{3}，-1}]∪[5，10）$ |
12．
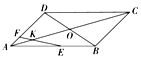如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）
如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）| A． | $\frac{8}{27}$ | B． | $\frac{1}{3}$ | C． | $\frac{10}{27}$ | D． | $\frac{11}{27}$ |
19．已知复数z=（3a+2i）（b-i）的实部为4，其中a、b为正实数，则2a+b的最小值为（ ）
| A． | 2 | B． | 4 | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |
16．“a≥3${∫}_{0}^{\frac{π}{6}}$cosθdθ”是“直线l：2ax-y+2a2=0（a＞0）与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的右支无交点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
13．已知复数z满足（3-4i）z=1+2i（i为虚数单位），则z的共轭复数是（ ）
| A． | -$\frac{1}{5}-\frac{2}{5}$i | B． | $-\frac{1}{5}+\frac{2}{5}i$ | C． | $\frac{1}{5}+\frac{2}{5}$i | D． | $\frac{1}{5}-\frac{2}{5}$i |