题目内容
3．
如图，D，C，B三点在地面同一直线上，从地面上C，D两点望山顶A，测得它们的仰角分别为45°和30°，已知CD=200米，点C位于BD上，则山高AB等于（ ）
| A． | 100$\sqrt{2}$米 | B． | 50（$\sqrt{3}$+1）米 | C． | $100（{\sqrt{3}+1}）$米 | D． | 200米 |
分析 直角△ABC与直角△ABD有公共边AB，若设AB=x，则在直角△ABC与直角△ABD就满足解直角三角形的条件，可以用x表示出BC与BD的长，根据BD-BC=CD，即可列方程求解．
解答 解：设AB=x米，在直角△ACB中，∠ACB=45°，
∴BC=AB=x米．
在直角△ABD中，∠D=30°，BD=$\sqrt{3}$x，
∵BD-BC=CD，
∴$\sqrt{3}$x-x=200，
解得：x=100（$\sqrt{3}$+1）．
故选C．
点评 本题主要考查了解直角三角形的方法，解决的关键是注意到两个直角三角形有公共的边，利用公共边表示其它的量，从而把问题转化为方程问题．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA=PB，E，F分别是PA，PB的中点．
14．设[x]表示不小于实数x的最小整数，如[2.6]=3，[-3.5]=-3．已知函数f（x）=[x]2-2[x]，若函数F（x）=f（x）-k（x-2）+2在（-1，4]上有2个零点，则k的取值范围是（ ）
| A． | $[{-\frac{5}{2}，-1}）∪[2，5）$ | B． | $[{-1，-\frac{2}{3}}）∪[5，10）$ | C． | $（{-\frac{4}{3}，-1}]∪[5，10）$ | D． | $[{-\frac{4}{3}，-1}]∪[5，10）$ |
18．设x＞0，y＞0，满足$\frac{4}{y}$+$\frac{1}{x}$=4，则x+y的最小值为（ ）
| A． | 4 | B． | $\frac{9}{4}$ | C． | 2 | D． | 9 |
12．
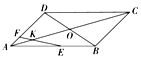如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）
如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）| A． | $\frac{8}{27}$ | B． | $\frac{1}{3}$ | C． | $\frac{10}{27}$ | D． | $\frac{11}{27}$ |
13．已知复数z满足（3-4i）z=1+2i（i为虚数单位），则z的共轭复数是（ ）
| A． | -$\frac{1}{5}-\frac{2}{5}$i | B． | $-\frac{1}{5}+\frac{2}{5}i$ | C． | $\frac{1}{5}+\frac{2}{5}$i | D． | $\frac{1}{5}-\frac{2}{5}$i |