题目内容
已知函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
)的图象关于y轴对称,则y=f(x)在下列哪个区间上是减函数( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的图像与性质
分析:根据函数f(x)的图象关于y轴对称,|θ|<
,可求出θ=-
,从而有f(x)=-2cos
x,即可求出函数f(x)在(-
,-
)上为减函数.
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
解答:
解:因为函数f(x)的图象关于y轴对称,所以当x=0时,f(x)取得最大(或最小)值,此时
f(x)=sinθ-
cosθ=2sin(θ-
),因为|θ|<
,所以,θ=-
,
所以f(x)=sin(
x-
)-
cos(
x-
)=2sin(
x-
)=-2cos
x,
所以函数f(x)在(-
,-
)上为减函数.
故选:B.
f(x)=sinθ-
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
所以f(x)=sin(
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
所以函数f(x)在(-
| π |
| 2 |
| π |
| 4 |
故选:B.
点评:本题主要考察了三角函数中的恒等变换应用,考察了三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
相关题目
设全集U=R,集合A={x|1<x<4},集合B={x|2≤x<5},则A∩(∁UB)=( )
| A、{x|1≤x<2} |
| B、{x|x<2} |
| C、{x|x≥5} |
| D、{x|1<x<2} |
已知实数x、y满足
,则目标函数z=x2+y2的最小值为( )
|
A、
| ||
| B、2 | ||
| C、1 | ||
| D、5 |

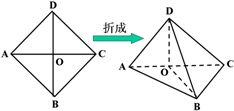 如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.