题目内容
下面给出的命题中:
①“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
②已知函数f(a)=∫
sinxdx,则f[f(
)]=1-cos1.
③已知ξ服从正态分布N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2.
④将函数y=cos2x的图象向右平移
个单位,得到函数y=sin(2x-
)的图象.
其中是真命题的有 .(填序号)
①“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
②已知函数f(a)=∫
a 0 |
| π |
| 2 |
③已知ξ服从正态分布N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2.
④将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
其中是真命题的有
考点:命题的真假判断与应用
专题:计算题,阅读型,三角函数的图像与性质,概率与统计,简易逻辑
分析:运用两直线垂直的条件,以及充分必要条件的定义,即可判断①;
由定积分运算法则和函数值的求法,即可判断②;
运用正态分布的特点,即曲线关于y轴对称,即可判断③;
运用三角函数图象左右平移,针对自变量x而言,以及诱导公式的运用,即可判断④.
由定积分运算法则和函数值的求法,即可判断②;
运用正态分布的特点,即曲线关于y轴对称,即可判断③;
运用三角函数图象左右平移,针对自变量x而言,以及诱导公式的运用,即可判断④.
解答:
解:对于①,直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直,则有
(m+2)(m-2)+m(m+2)=0,解得,m=-2或1,则应为充分不必要条件,则①错;
对于②,函数f(a)=∫
sinxdx=(-cosx)|
=1-cosa,则f[f(
)]=f(1)=1-cos1,则②对;
对于③,ξ服从正态分布N(0,σ2),曲线关于y轴对称,由P(-2≤ξ≤0)=0.4,
则P(ξ>2)=0.5-0.4=0.1,则③错;
对于④,将函数y=cos2x的图象向右平移
个单位,得到函数y=cos2(x-
),
即有y=sin(2x+
-
),即有y=sin(2x-
)的图象,则④对.
故答案为:②④
(m+2)(m-2)+m(m+2)=0,解得,m=-2或1,则应为充分不必要条件,则①错;
对于②,函数f(a)=∫
a 0 |
a 0 |
| π |
| 2 |
对于③,ξ服从正态分布N(0,σ2),曲线关于y轴对称,由P(-2≤ξ≤0)=0.4,
则P(ξ>2)=0.5-0.4=0.1,则③错;
对于④,将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
即有y=sin(2x+
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
故答案为:②④
点评:本题考查充分必要条件的判断和函数的定积分运算、正态分布曲线的特点、三角函数的图象平移规律,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
已知实数x、y满足
,则目标函数z=x2+y2的最小值为( )
|
A、
| ||
| B、2 | ||
| C、1 | ||
| D、5 |
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 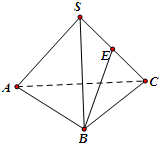
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |
已知正数x、y满足
,则z=(
)x•(
)y的最小值为( )
|
| 1 |
| 4 |
| 1 |
| 2 |
A、
| |||
B、
| |||
C、2
| |||
| D、4 |

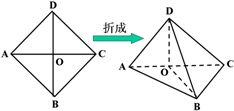 如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.