题目内容
若四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，BA⊥AD，PA⊥平面ABCD，则AB=AP=AD=3，CD=6，则直线PD和BC成的角的大小为 ．
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：先作出异面直线所成的角，再使用余弦定理即可求出．
解答：
解：建立坐标系如图：
因为底面ABCD为直角梯形，AB∥CD，BA⊥AD，PA⊥平面ABCD，则AB=AP=AD=3，CD=6，
所以P（0，0，3），D（0，3，0），B（3，0，0），C（6，3，0），
所以
=（0，3，-3），
=（3，3，0），
所以cos＜
，
＞=
=
=
，
所以直线PD和BC成的角的大小为
；
故答案为：
．
因为底面ABCD为直角梯形，AB∥CD，BA⊥AD，PA⊥平面ABCD，则AB=AP=AD=3，CD=6，
所以P（0，0，3），D（0，3，0），B（3，0，0），C（6，3，0），
所以
| PD |
| BC |
所以cos＜
| PD |
| BC |
| ||||
|
|
| 9 | ||||
|
| 1 |
| 2 |
所以直线PD和BC成的角的大小为
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查了异面直线所成的角的求法；本题借助于空间向量的数量积解答的；关键是适当的建立坐标系，正确写出向量的坐标和正确的计算．
练习册系列答案
相关题目
在等差数列{an}中，a4=7，a1+a5=10，则公差d=（ ）
| A、1 | B、2 | C、3 | D、4 |
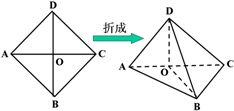如图，以正方形ABCD的对角线AC为折痕，使△ADC和△ABC折成相垂直的两个面，点O为AC的中点．
已知椭圆