题目内容
已知直线y=ax+1与双曲线3x2-y2=1相交于A、B两点,是否存在这样的实数a,使得A、B关于直线y=2x对称?如果存在,求出a的值,如果不存在,说明理由.
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:由
,消去y,得(3-a2)x2-2ax-2=0,假设存在实数a,使得A,B关于y=2x对称,则直线y=ax+1与y=2x垂直,a=-
,直线l的方程为y=-
x+1,由此能推导出不存在实数a使A,B关于直线y=2x对称.
|
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由
,消去y,得(3-a2)x2-2ax-2=0,
设A(x1,y1),B(x2,y2),则
,(*)
假设存在实数a,使得A,B关于y=2x对称,则直线y=ax+1与y=2x垂直,
∴a=-
,直线l的方程为y=-
x+1,
把a=-
代入(*),得x1+x2=-
,
∴AB中点的横坐标为x=-
,纵坐标为y=-
×(-
)+1=
,
∵AB中点(-
,
)不在直线y=2x上,
∴不存在实数a使A,B关于直线y=2x对称.
|
设A(x1,y1),B(x2,y2),则
|
假设存在实数a,使得A,B关于y=2x对称,则直线y=ax+1与y=2x垂直,
∴a=-
| 1 |
| 2 |
| 1 |
| 2 |
把a=-
| 1 |
| 2 |
| 4 |
| 11 |
∴AB中点的横坐标为x=-
| 2 |
| 11 |
| 1 |
| 2 |
| 2 |
| 11 |
| 12 |
| 11 |
∵AB中点(-
| 2 |
| 11 |
| 12 |
| 11 |
∴不存在实数a使A,B关于直线y=2x对称.
点评:本题考查满足条件的实数是否存在的判断与求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
下列函数中,是奇函数,又在定义域内为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=-2x3 | ||
| D、y=log2(-x) |
在等差数列{an}中,a4=7,a1+a5=10,则公差d=( )
| A、1 | B、2 | C、3 | D、4 |
设全集U=R,集合A={x|1<x<4},集合B={x|2≤x<5},则A∩(∁UB)=( )
| A、{x|1≤x<2} |
| B、{x|x<2} |
| C、{x|x≥5} |
| D、{x|1<x<2} |
在复平面内,复数
对应的点位于( )
| 1+i |
| (1-i)2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

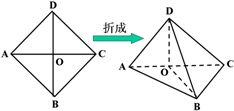 如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.