题目内容
(1)若
,
,
成等差,求n的值;
(2)求证:
=
(其中n≥k≥2,k∈N);
(3)数列{xn}是首项为x1,公比为q的等比数列,其前n项和为Sn,化简下列式子:Tn=S1
+S2
+…+Sn
.
| C | 1 n |
| C | 2 n |
| C | 3 n |
(2)求证:
| ||
| n |
| ||
| k |
(3)数列{xn}是首项为x1,公比为q的等比数列,其前n项和为Sn,化简下列式子:Tn=S1
| C | 1 n |
| C | 2 n |
| C | n n |
考点:二项式定理的应用,等差数列的通项公式,数列的求和,组合及组合数公式
专题:等差数列与等比数列,排列组合,二项式定理
分析:(1)利用等差数列的中项,结合组合数公式,进行化简即可;
(2)利用组合数公式,进行化简证明即可;
(3)讨论当q=1时,和q≠1时,求出等比数列的Sn,再分别进行计算与化简.
(2)利用组合数公式,进行化简证明即可;
(3)讨论当q=1时,和q≠1时,求出等比数列的Sn,再分别进行计算与化简.
解答:
解:(1)∵
,
,
成等差,
∴2
=
+
,
即
=n+
,
解得n=7或n=2(舍),
∴n=7;
(2)证明:∵n≥k≥2,
∴
=
=
,
∴
=
(其中n≥k≥2,k∈N);
(3)∵数列{xn}是首项为x1,公比为q的等比数列,其前n项和为Sn,
∴①当q=1时,Sn=nx1,
∴Sk•
=kx1•
=x1•k•
=nx1•
=nx1•
,
∴S1Cn1+S2Cn2+S3Cn3+S4Cn4+…+SnCnn
=na1(Cn-10+Cn-11+Cn-12+…+Cn-1n-1)=na12n-1;
②当q≠1时,Sn=
,
∴Sk•
=
•
=
•
-
qk
∴S1Cn1+S2Cn2+S3Cn3+S4Cn4+…+SnCnn
=
(
+
+
+…+
)-
(
•q+
•q2+
•q3+…+
•qn)
=
•(2n-1)-
•[(1+q)n-1]
=
[2n-(1+q)n].
| C | 1 n |
| C | 2 n |
| C | 3 n |
∴2
| C | 2 n |
| C | 1 n |
| C | 3 n |
即
| 2n(n-1) |
| 2×1 |
| n(n-1)(n-2) |
| 3×2×1 |
解得n=7或n=2(舍),
∴n=7;
(2)证明:∵n≥k≥2,
∴
| ||
| n |
| n(n-1)(n-2)…(n-k+1) |
| n×k×(k-1)×…×3×2×1 |
| ||
| k |
∴
| ||
| n |
| ||
| k |
(3)∵数列{xn}是首项为x1,公比为q的等比数列,其前n项和为Sn,
∴①当q=1时,Sn=nx1,
∴Sk•
| C | k n |
| C | k n |
| n! |
| k!•(n-k)! |
| (n-1)! |
| (k-1)!•(n-k)! |
| C | k-1 n-1 |
∴S1Cn1+S2Cn2+S3Cn3+S4Cn4+…+SnCnn
=na1(Cn-10+Cn-11+Cn-12+…+Cn-1n-1)=na12n-1;
②当q≠1时,Sn=
| x1(1-qn) |
| 1-q |
∴Sk•
| C | k n |
| x1(1-qk) |
| 1-q |
| C | k n |
| x1 |
| 1-q |
| C | k n |
| x1 |
| 1-q |
| C | k n |
∴S1Cn1+S2Cn2+S3Cn3+S4Cn4+…+SnCnn
=
| x1 |
| 1-q |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| x1 |
| 1-q |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
=
| x1 |
| 1-q |
| x1 |
| 1-q |
=
| x1 |
| 1-q |
点评:本题考查了组合及组合数公式的应用问题,也考查了等差与等比数列的性质与前n项和等知识的应用问题,是难题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知函数f(x)=
,若对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是( )
| ex+m |
| ex+1 |
A、[
| ||
| B、[0,1] | ||
| C、[1,2] | ||
D、[
|
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是( )
| A、(-∞,-2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[1,+∞) |
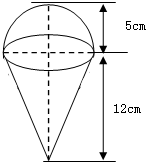 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)