题目内容
已知函数f(x)=
,若对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是( )
| ex+m |
| ex+1 |
A、[
| ||
| B、[0,1] | ||
| C、[1,2] | ||
D、[
|
考点:指数函数单调性的应用
专题:函数的性质及应用
分析:把函数化为函数f(x)=
=1+
,分类讨论得出值域,根据端点值,f(a)+f(b)>f(c)成立,最小值的2倍与最大值的比较,列出不等式即可求解.
| ex+m |
| ex+1 |
| m-1 |
| ex+1 |
解答:
解:∵函数f(x)=
,
∴函数f(x)=
=1+
,
∵ex+1>1,
∴0<
<1,
①当m=1时,f(x)=1,对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立
②当m>1时,∵0<
<m-1,
1<1+
<m,
∴对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立
即有只需:2≥m,
∴1<m≤2,
③当m<1时,m-1<
<0,
∴m<1+
<1,
∴对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,即只需2m≥1,
≤m<1,
综上所述实数m的取值范围为:[
,2],
| ex+m |
| ex+1 |
∴函数f(x)=
| ex+m |
| ex+1 |
| m-1 |
| ex+1 |
∵ex+1>1,
∴0<
| 1 |
| ex+1 |
①当m=1时,f(x)=1,对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立
②当m>1时,∵0<
| m-1 |
| ex+1 |
1<1+
| m-1 |
| ex+1 |
∴对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立
即有只需:2≥m,
∴1<m≤2,
③当m<1时,m-1<
| m-1 |
| ex+1 |
∴m<1+
| m-1 |
| ex+1 |
∴对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,即只需2m≥1,
| 1 |
| 2 |
综上所述实数m的取值范围为:[
| 1 |
| 2 |
点评:本题考查了不等式的恒成立问题与函数单调性,结合不等式的性质转化求解问题,难度较大,属于思维量大的题目

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)=
,则f(2012)=( )
|
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
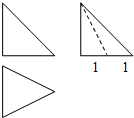 一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为
一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为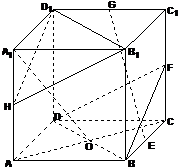 正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点.
正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点.