题目内容

已知函数y=2sin（2x+
π
6
）．
（1）求函数在区间[
π
6
，
π
3
]的单调性；
（2）若x∈[
π
6
，
π
3
]，求函数的最大值和最小值．
考点：正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：（1）令2kπ+
π
2
≤2x+
π
6
≤2kπ+
3π
2
，k∈z，可求得kπ+
π
6
≤x≤kπ+
2π
3
，k∈z，当k=0时，有[
π
6
，
π
3
]?[
π
6
，
2π
3
]，从而有函数在区间[
π
6
，
π
3
]的单调递减．
（2）由（1）知，函数在区间[
π
6
，
π
3
]的单调递减．从而可得f（x）maz=f（
π
6
）=2，f（x）min=f（
π
3
）=1．
解答： 解：（1）对于函数y=2sin（2x+
π
6
），令2kπ+
π
2
≤2x+
π
6
≤2kπ+
3π
2
，k∈z，
求得kπ+
π
6
≤x≤kπ+
2π
3
，k∈z
当k=0时，有[
π
6
，
π
3
]?[
π
6
，
2π
3
]
故函数在区间[
π
6
，
π
3
]的单调递减．
（2）由（1）知，函数在区间[
π
6
，
π
3
]的单调递减．
故f（x）maz=f（
π
6
）=2，f（x）min=f（
π
3
）=1．
点评：本题主要考察了正弦函数的图象和性质，属于基本知识的考查．
练习册系列答案
相关题目
已知函数f（x）=
x2+a
x+b
，（a，b∈R），若f（x）为奇函数，且f（1）=5．
（1）求函数f（x）的解析式；
（2）用定义判断f（x）在（0，+∞）上的单调性，并写出相应的单调区间．
某区为了解全区2800名九年级学生英语口语考试成绩的情况，从中随机抽取了部分学生的成绩（满分24分，得分均为整数），制成下表：
分数段
（x分）		x≤1617≤x≤1819≤x≤2021≤x≤2223≤x≤24
人 数101535112128
（1）填空：
①本次抽样调查共抽取了
 
名学生；
②学生成绩的中位数落在
 
分数段；
③若用扇形统计图表示统计结果，则分数段为x≤16的人数所对应扇形的圆心角为
 
°；
（2）如果将21分以上（含21分）定为优秀，请估计该区九年级考生成绩为优秀的人数．
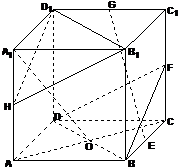正方体ABCD-A1B1C1D1中，F，H分别为棱CC1，AA1的中点，O为AC与BD的交点．
（1）平面BDF∥平面B1D1H；
（2）A1O⊥平面BDF；
（3）平面A1BD⊥平面BDF．
已知在平面直角坐标系中，O为坐标原点，给定两点A（1，0），B（0，-2），点C满足
OC
=α
OA
+β
OB
，其中α，β∈R，且α-2β=1．
（1）求点C的轨迹方程；
（2）设点C的轨迹与双曲线
x2
a2
-y2=13，（a＞0）交于两点M，N，且OM⊥ON，求该双曲线的方程．
如图：已知PA⊥平面ABC，AB是⊙O的直径，C是圆上的任意一点，求证：PC⊥BC．
已知，圆锥的全面积是3π，底面积是π，则它的体积是
 
．
（1）若
C
1
n
，
C
2
n
，
C
3
n
成等差，求n的值；
（2）求证：
C
k
n
n
=
C
k-1
n-1
k
(其中n≥k≥2，k∈N)；
（3）数列{xn}是首项为x1，公比为q的等比数列，其前n项和为Sn，化简下列式子：Tn=S1
C
1
n
+S2
C
2
n
+…+Sn
C
n
n
．
已知sin（π-x）=2cosx，则sin2x+1=（　　）
A、
6
5
B、
4
3
C、
5
3
D、
9
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网