题目内容
若关于x的方程1+
=2logx2有两解，则实数a的取值范围是 ．
| log2(2lga-x) |
| log2x |
考点：函数的零点与方程根的关系
专题：计算题
分析：解方程转化为x2-2xlga+4=0，根据△＞0，解出即可．
解答：
解：∵1+
=2logx2，
∴
+
=2，
∴x2-2xlga+4=0，
∴△=4lg2a-16＞0，
解得：a＞100或0＜a＜
，
故答案为：{a|a＞100或0＜a＜
}．
| log2(2lga-x) |
| log2x |
∴
| log | x 2 |
| log | (2lga-x) 2 |
∴x2-2xlga+4=0，
∴△=4lg2a-16＞0，
解得：a＞100或0＜a＜
| 1 |
| 100 |
故答案为：{a|a＞100或0＜a＜
| 1 |
| 100 |
点评：本题考查了解方程问题，考查了对数，指数的互化问题，是一道基础题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
设a=log
0.6，b=log20.6，c=20.6，则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| A、a＜b＜c |
| B、b＜c＜a |
| C、b＜a＜c |
| D、c＜a＜b |
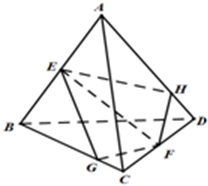如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，下列判断中：