题目内容
证明:(2-cos2x)(2+tan2x)=(1+2tan2x)(2-sin2x).
考点:三角函数恒等式的证明
专题:证明题,三角函数的求值
分析:由二倍角的正弦、余弦公式,万能公式化简后可得左边等于右边,从而得证.
解答:
证明:设t=tanx,
左边=(2-
)(2+t2)=
×(2+t2)=
=
.
右边=(1+2t2)(2-
)═(1+2t2)×
=
=左边.
故得证.
左边=(2-
| 1+cos2x |
| 2 |
3-
| ||
| 2 |
| (1+2t2)(2+t2) |
| 1+t2 |
| 2+5t2+2t4 |
| 1+t2 |
右边=(1+2t2)(2-
| 1-cos2x |
| 2 |
3+
| ||
| 2 |
| 2+5t2+2t4 |
| 1+t2 |
故得证.
点评:本题主要考察了三角函数恒等式的证明,熟练运用二倍角的正弦、余弦公式,万能公式是关键,属于基础题.

练习册系列答案
相关题目
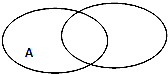
如图中阴影部分表示的集合是( )


| A、∁U(A∪B) |
| B、A∩(∁UB) |
| C、∁U(A∩B) |
| D、∁B(A∩B) |
 已知A=
已知A=