题目内容
已知椭圆C:
+
=1(a>b>0)的两个焦点分别是 F1,F2,斜率为k的直线l过左焦点F1且与椭圆的交点分别为A、B,与y轴交点为C,又B为线段CF1的中点,若|k|≤
,求椭圆离心率e的取值范围 .
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先求出B点坐标,代入椭圆方程得到:
+
=1,结合a2=b2+c2,e=
得到方程
+e2-5≤
,解出即可.
| c2 |
| 4a2 |
| k2c2 |
| 4b2 |
| c |
| a |
| 4 |
| e2 |
| 7 |
| 2 |
解答:
解:过F1(-c,0),设y=k(x+c)(k≠0),将x=0代入,y=kc,所以C(0,kc),
B是F1C中点,B(-
,
),B在椭圆上,将B代入椭圆方程,
得:
+
=1,
∴b2c2+k2 a2 c2=4a2 b2,
∴(a2-c2)c2+k2 a2 c2=4a2 (a2-c2),
∴k2 a2 c2=4a4+c4-5a2 c2,
∴k2=
,且e=
,
∴k2=
+e2-5,又∵k2≤
,
∴
+e2-5≤
,解得:
≤e<1,
故答案为:[
,1).
B是F1C中点,B(-
| c |
| 2 |
| kc |
| 2 |
得:
| c2 |
| 4a2 |
| k2c2 |
| 4b2 |
∴b2c2+k2 a2 c2=4a2 b2,
∴(a2-c2)c2+k2 a2 c2=4a2 (a2-c2),
∴k2 a2 c2=4a4+c4-5a2 c2,
∴k2=
| 4a4+c4-5a2c2 |
| a2c2 |
| c |
| a |
∴k2=
| 4 |
| e2 |
| 7 |
| 2 |
∴
| 4 |
| e2 |
| 7 |
| 2 |
| ||
| 2 |
故答案为:[
| ||
| 2 |
点评:本题考查了椭圆的性质,考查了转化思想,考查了方程问题,是一道中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知全集U={1,2,3,4,5},集合A={1,2,3},B={3,4,5},图中阴影部分所表示的集合为( )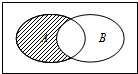

| A、{3} |
| B、{1,2} |
| C、{4,5} |
| D、{1,2,3,4,5} |
如图中阴影部分表示的集合是( )


| A、∁U(A∪B) |
| B、A∩(∁UB) |
| C、∁U(A∩B) |
| D、∁B(A∩B) |
下列函数中,为奇函数的是( )
A、f(x)=
| ||
| B、f(x)=lnx | ||
| C、f(x)=2π | ||
| D、f(x)=sinx |
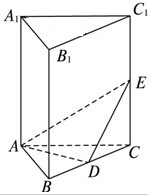 已知在直三棱柱ABC-A1B1C1中,E为CC1上任意一点,D在BC上(点D不同于点C),AD⊥DE,求证:平面ADE⊥平面BCC1B1.
已知在直三棱柱ABC-A1B1C1中,E为CC1上任意一点,D在BC上(点D不同于点C),AD⊥DE,求证:平面ADE⊥平面BCC1B1.