题目内容
已知tanα=-
,则
-sinαcosα-2cos2α= .
| 1 |
| 2 |
| 1 |
| sin2α |
考点:二倍角的余弦,三角函数的化简求值,二倍角的正弦
专题:三角函数的求值
分析:原式分子、分母看做“1”,利用同角三角函数间基本关系化简,再弦化切后将tanα的值代入计算即可求出值.
解答:
解:∵tanα=-
,
∴原式=
-
=
-
=
-
=-
.
故答案为:-
.
| 1 |
| 2 |
∴原式=
| sin2α+cos2α |
| 2sinαcosα |
| sinαcosα+2(-sin2α+cos2α) |
| sin2α+cos2α |
=
| tan2α+1 |
| 2tanα |
| tanα+2(-tan2α+1) |
| tan2α+1 |
=
| ||
-2×
|
-
| ||||
|
=-
| 41 |
| 20 |
故答案为:-
| 41 |
| 20 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知集合A={1,2,3},B={2,3,4,5},则A∪B=( )
| A、{6,7,8} |
| B、{1,4,5,6,7,8} |
| C、{2,3} |
| D、{1,2,3,4,5} |
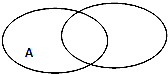
如图中阴影部分表示的集合是( )


| A、∁U(A∪B) |
| B、A∩(∁UB) |
| C、∁U(A∩B) |
| D、∁B(A∩B) |
若集合{0,a2,a+b}={1,a,
},则a2012+b2011的值为( )
| b |
| a |
| A、0 | B、1 | C、-1 | D、±1 |
 已知A=
已知A=