题目内容
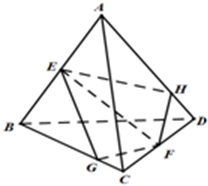 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中:
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中:①对于任意的平面α,都有S△EFG=S△EFH;
②存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上;
③对于任意的平面α,都有直线GF,EH,BD相交于同一点或相互平行;
④对于任意的平面α,当G,H在线段BC,AD上时,几何体AC-EGFH的体积是一个定值.
其中正确的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:作图题,探究型,空间位置关系与距离
分析:①分别取AC、BD的中点J、I,利用线面平行的性质可知AD与BC到平面IEJF的距离相等,从而可判断①;
②,当点G在BC上移动时,点H在AD之间移动,可判断②;
③,G、H分别为相应线段中点时,三线平行,若G、H不是相应线段中点时,三线相交于一点,可判断③;
④,当H为D,G为C时,此时几何体的体积为三棱锥A-CDE的体积,为该四面体体积的一半,结合①的结论,可判断④.
②,当点G在BC上移动时,点H在AD之间移动,可判断②;
③,G、H分别为相应线段中点时,三线平行,若G、H不是相应线段中点时,三线相交于一点,可判断③;
④,当H为D,G为C时,此时几何体的体积为三棱锥A-CDE的体积,为该四面体体积的一半,结合①的结论,可判断④.
解答:
解:对于①,分别取AC、BD的中点J、I,则BC∥平面MENF,AD∥平面IEJF,且AD与BC到平面IEJF的距离相等,因此对于任意的α,都有S△EFG=S△EFH,故①正确;
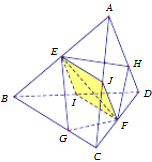
对于②,当点G与点B重合时,点H与点A重合,当点G与点C重合时,点H与点D重合,故当点G在BC上移动时,点H在AD之间移动,故不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,即②错误;
对于③,G、H分别为相应线段中点时,三线平行,若G、H不是相应线段中点时,三线相交于一点,即对于任意的平面α,都有直线GF,EH,BD相交于同一点或相互平行,③正确;
对于④,当H为D,G为C时,此时几何体的体积为三棱锥A-CDE的体积,为该四面体体积的一半,
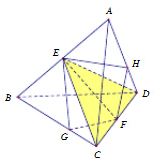
如图,只需证VC-EFG=VD-EFH,由①知,只需证C、D到截面的距离相等,
∵F为CD的中点,
∴C、D到截面的距离相等,故几何体AC-EGFH的体积是一个定值,即④正确;
综上所述,正确的为①③④,有3个,
故选:B.

对于②,当点G与点B重合时,点H与点A重合,当点G与点C重合时,点H与点D重合,故当点G在BC上移动时,点H在AD之间移动,故不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,即②错误;
对于③,G、H分别为相应线段中点时,三线平行,若G、H不是相应线段中点时,三线相交于一点,即对于任意的平面α,都有直线GF,EH,BD相交于同一点或相互平行,③正确;
对于④,当H为D,G为C时,此时几何体的体积为三棱锥A-CDE的体积,为该四面体体积的一半,

如图,只需证VC-EFG=VD-EFH,由①知,只需证C、D到截面的距离相等,
∵F为CD的中点,
∴C、D到截面的距离相等,故几何体AC-EGFH的体积是一个定值,即④正确;
综上所述,正确的为①③④,有3个,
故选:B.
点评:本题考查线面平行的判定与性质,考查共面定理、三角形的中位线定理、考查作图能力与分析、推理能力,空间想象能力,属于难题.

练习册系列答案
相关题目
下列函数中,为奇函数的是( )
A、f(x)=
| ||
| B、f(x)=lnx | ||
| C、f(x)=2π | ||
| D、f(x)=sinx |
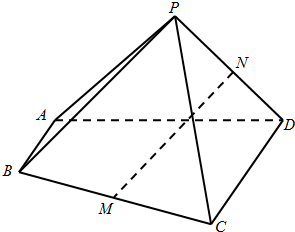 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.