题目内容
如图，两个完全相等的正方形ABCD和ABEF不在同一平面，点M，N分别在他们的对角线AC，BF上，且CM=BN，求证：MN∥平面BCE．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：过点M作MP⊥AB，交AB与点P，连接NP，证明平面PMN∥平面BCE，再证明MN∥平面BCE即可．
解答：
解：过点M作MP⊥AB，交AB与点P，连接NP，如图所示，
∴MP∥CB，
∴
=
；
又∵BF=AC，CM=BN，
∴FN=AM，
∴
=
，
∴PN∥BE；
又∵BE?平面BCE，PN?平面BCE，
∴PN∥平面BCE，
同理，PM∥平面BCE；
又PM∩PN=P，PM?平面PMN，PN?平面PMN，
∴平面PMN∥平面BCE；
∵MN?平面PMN，
∴MN∥平面BCE．
∴MP∥CB，
∴
| AM |
| CM |
| AP |
| BP |
又∵BF=AC，CM=BN，
∴FN=AM，
∴
| AP |
| BP |
| FN |
| BN |
∴PN∥BE；
又∵BE?平面BCE，PN?平面BCE，
∴PN∥平面BCE，
同理，PM∥平面BCE；
又PM∩PN=P，PM?平面PMN，PN?平面PMN，
∴平面PMN∥平面BCE；
∵MN?平面PMN，
∴MN∥平面BCE．
点评：本题考查了直线与平面平行的判定问题，解题时应先证明面面平行，再证明线面平行，是中档题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
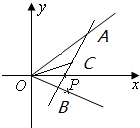如图所示，射线OA、OB分别与x轴正半轴成45°和30°角，过点P（1，0）作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y=
如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥平面ABCD，PA=AB，M、N分别是线段PB、AC上的动点，且不与端点重合，PM=AN．
在正方体ABCD-A1B1C1D1中，与AC平行，且过正方体三个顶点的截面是